“单元整体教学”理念下的高中数学教学设计
作者: 时辉
[摘 要] “单元整体教学”是新课改的必然趋势. 研究者以“圆锥曲线的方程”为例,从“旧知回顾,搭建知识框架”“加强探索,初步构建新知”“立足框架,促使方程形成”“课堂总结,完善框架结构”四个方面展开单元整体教学设计,并结合本节课的教学谈几点反思.
[关键词] 单元整体教学;圆锥曲线;教学反思
随着新课改的推进,“单元整体教学”受到广大教育工作者的关注. 单元整体教学不仅可以帮助学生更好地规划数学学科核心素养的发展,还能在大问题、大框架、大背景下对学生进行高观点统领,对知识形成结构性关联,规避传统授课模式的碎片化现象的发生. 究竟该如何实施单元整体教学呢?本文以“圆锥曲线的方程”为例展开设计与反思.
教学过程设计
1. 旧知回顾,搭建知识框架
(1)问题引领,搭建单元框架
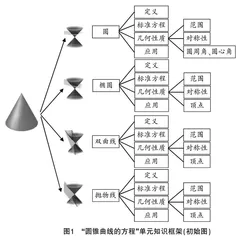
课堂伊始,引导学生回顾直线与圆的方程,根据“圆锥曲线的方程”这个标题类比圆锥曲线的定义. 在问题的启发下,借助多媒体进行图象的动态演示,具体内容为:用一个平面去截两个互为倒立的圆锥体,通过调整平面与圆锥体的位置关系,形成不同的截面和截口曲线,让学生从截口曲线中发现圆、椭圆、双曲线与抛物线. 同时借助信息技术建构相应的知识框架图(见图1).
设计意图 引导学生从直线与圆的方程出发,对圆锥曲线的方程进行类比,借助信息技术帮助学生初步架构单元知识框架,让学生对本单元将要探索的内容做到心中有数. 随着知识框架的形成,学生基本明确了单元知识结构.
(2)明晰重点,渗透研究方法
带领学生回顾圆的学习过程,平面直角坐标系的建立与圆的标准方程的形成,对揭露圆的几何性质具有重要价值. 简而言之,就是将平面解析几何中的平面图形置于平面直角坐标系内,可促进标准方程的形成,且对几何性质与应用的研究具有重要意义,由此可见“坐标法”的重要性.
同样,“坐标法”对本单元教学也有重要价值,师生共同探索,发现可借助“坐标法”来研究圆锥曲线相关知识.
设计意图 类比圆的研究方法,为引出“坐标法”服务. 这是借助从特殊到一般思想研究平面解析几何的重要方法.
2. 加强探索,初步构建新知
(1)温习旧知,联系教学内容
关于椭圆概念的研究,首先要让学生明确椭圆是一个经过拉伸、压缩的圆. 本节课可从圆出发探索与椭圆相关的知识,如利用“一问一答”的方法,温习圆的定义以及画法,使学生结合圆的定义猜想:将圆拉伸、压缩后,圆心O就变成了点O与O′(如图2所示). 在复习圆的定义的基础上,探索椭圆.
设计意图 很多时候,学科的发展源于猜想,猜想是创新的源头. 结合猜想进行数学实验研究或运算,可验证猜想的准确性. 事实证明,猜想是促进数学发展不可或缺的一个环节,是“授学生以渔”的过程. 学生结合获得的知识框架,自主投入椭圆的研究过程. 同时,此环节还渗透了重要的数形结合思想方法,对发展学生的思维起着重要作用.
(2)实操探索,形成新知
活动准备:课前准备好图钉、棉线、铅笔、小环等材料.
活动安排:以小组合作学习的方式,引导学生固定棉线的两点画椭圆,学生在自主探索过程中发现两点间的距离的长短会影响画椭圆的结论,通过圆的定义的类比获得椭圆的定义. 而后借助多媒体的演示功能,带领学生观察椭圆的绘制过程,明确椭圆上任意一点所满足的条件是什么.
设计意图 在猜想的基础上,以实操活动加上验证探索,一方面可以培养学生的动手动脑能力,另一方面可以增强学生的学习体验与团队合作能力. 实操活动的开展意在引导学生自主概括椭圆的概念,发展学生的数学直观想象和抽象素养.
设计意图 确定椭圆焦点、焦距与半焦距等核心概念之后,抛出上述问题意在启发学生思维,使学生在思考中有所收获.
在获得上述结论的基础上,教师带领学生用多媒体加以验证,以进一步深化学生对这个结论的理解.
设计意图 “猜想—实验—验证”是学习数学新知常用的方法,借助信息技术验证结论,可帮助学生获得严谨的数学精神,这样建构的知识也会保持得更加长久,形成的研究方法、数学思想等能让学生受益终身.
3. 立足框架,促使方程形成
(1)齐心探索,建立方程
课堂伊始已经搭建了单元知识框架,学生结合框架要点研究完定义之后,则需要将图形置于坐标系中探索方程,为揭露图形的几何性质与应用奠定基础. 此环节,采用小组合作学习的方式借助类比思想与圆的研究方法作比较,分析平面直角坐标系的建立方法,以获得椭圆的方程.
设计意图 立足单元教学的整体思想,将教学明线(定义—标准方程—几何性质—应用)与暗线(坐标法、数形结合思想方法等)交织在一起,促使学生自主发现建立平面直角坐标系的关键点,并借助多媒体的演示功能,进一步促进椭圆的标准方程的建立. 在此过程中,学生掌握了椭圆标准方程中的a,b,c的几何意义,为接下来的应用奠定了基础.
(2)过程类比,方程推导
师:前面我们探索了焦点在x轴上时椭圆的标准方程,现在请大家类比前面的研究方法,采用合作学习的方式推导焦点在y轴上时椭圆的标准方程. 组内互相检查推导过程,并派一名代表来展示. 着重介绍方程推导的步骤在不同情况下的异同点,探寻最简洁的推导方法.
完成上述探索,学生自主提炼出判断椭圆的焦点在x轴上还是在y轴上的结论:若椭圆的标准方程中x2下的分母大一些,可确定该椭圆的焦点在x轴上;若y2下的分母大一些,可确定该椭圆的焦点在y轴上.
设计意图 此环节不仅检查学生对椭圆的标准方程推导过程的理解程度,还通过类比思想的渗透,促使学生形成良好的数学抽象、数学建模等能力. 简便方法的探寻,具有优化学生数学思维,促使学生学会从不同视角观察与分析问题的作用. 对探索内容的总结,可进一步提升学生的归纳能力,为后续解题夯实基础.
(3)例题分析,巩固新知
求解此题,首先要准确判断题干信息所揭露的椭圆焦点究竟在哪个坐标轴上,若条件中没有明确给出,则需要分类讨论. 结合关键点先设好椭圆的标准方程,然后分析方程中a,b的值,再以小组讨论的方式探寻不同的解题方法.
例2 若椭圆分别过点Q(0,-3),P(-2,2),请写出该椭圆的标准方程.
解决此题的关键在于判断椭圆的焦点究竟在哪个坐标轴上,若条件没有明确给出,同样需要分类讨论. 因为有例1的求解经验,学生求解此题时就显得比较轻松,为了深化学生的理解,特别强调当a,b的值确定后,需要观察它们是否满足a>b>0这个条件.
例3 完成如下练习.
(1)椭圆25x2+16y2=9的焦点坐标是什么?
(2)符合下列条件的椭圆的标准方程分别是什么?
设计意图 例1属于经典问题,意在引导学生分别应用定义法、待定系数法解题,达到触类旁通的目的;例2在例1的基础上引导学生探寻求解椭圆的标准方程的通法,培养学生的数学运算素养和逻辑推理能力;例3以由浅入深的问题进一步巩固学生的知识结构,促使学生在解题过程中完善知识体系.
4. 课堂总结,完善框架结构
以“开火车”的方式,要求每一个学生说一点在本节课的收获与感悟,避免重复. 根据学生的总结与收获进一步完善课堂伊始建立的知识框架图,并以类比的方式让学生感知圆是一种特殊的椭圆,从而提炼出三种圆锥曲线. 同时教师借助多媒体展示“圆锥曲线的方程”单元知识框架图(如图3所示).
设计意图 以小游戏“开火车”的方式进行归纳总结,一方面提升学生的学习热情,获得研究一类问题的能力;另一方面让学生查漏补缺,进一步完善知识体系,发展数学学科核心素养.
教学反思
1. 教学目标的反思
从教学目标的设置来看,单元教学设计需利用整体思想,引导学生从单元知识框架、思想方法等角度了解教学内容. 本节课的教学,在发展学生数学学科核心素养的基础上设计了与学生实际认知水平相匹配的目标.
2. 教学内容的反思
掌握知识整体框架和内部间的逻辑关系,让学生从整体上深度学习相应的知识. 本单元主要涵盖椭圆、双曲线与抛物线三个模块的内容,因此在实施单元教学前,可从整体的角度建构单元知识框架,并以思维导图的方式展现出来,让学生对将要学习的内容能一目了然.
3. 教学策略的反思
课堂是教师、学生与教材三者和谐统一的场地,将三者有机地融为一体,制定有效的教学策略,可进一步开发学生的思维,帮助学生更好地提炼数学思想方法. 本节课,教师通过明线和暗线的布置,借助多媒体帮助学生从真正意义上掌握椭圆的标准方程的推导方法,为后续研究类似问题奠定了基础.
总之,开展单元教学是帮助学生建构完整知识结构的重要途径. 教师应在充分了解教情与学情的基础上设计教学方案,以优化学生的思维,发展学生的数学学科核心素养.
作者简介:时辉(1985—),本科学历,中学一级教师,从事高中数学教学工作.