基于深度学习的数学教学研究

［摘  要］ 深度学习与浅层学习有着质的区别，它具有批判性、迁移性与主动性等特征. 文章以“双曲线及其标准方程”的教学为例，具体谈谈教师该如何在教学中进行思路点拨，让深度学习真实发生，并提出深度学习需要批判性地应用理科思维，深度学习可促进数学思想方法的提炼，深度学习有利于学生掌握数学知识本质.

［关键词］ 深度学习；教学；思维

深度学习是指在理解学习的基础上，学习者能够批判性地学习新的思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，作出决策和解决问题的学习［1］. 在新课改背景下，核心素养是教学的终极目标，而高中数学具有抽象程度高、逻辑性强等特点，这就要求教师从学情出发，引导学生把握好数学的本质，领会数学思想方法，以促进高阶思维的发展.

深度学习概述

1. 深度学习的发展

美国教育家布鲁姆将教育目标分为“认知、情感、动作技能”三大领域，同时将人的认知由低到高分成“知识、领会、应用、分析、综合、评价”六个层次. 其中浅层学习对应认知的“知识与领会”两个层次，而深度学习则对应认知的“应用、分析、综合、评价”四个层次.

2. 深度学习与浅层学习的对比

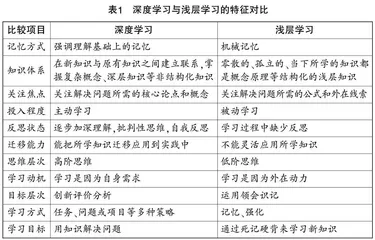
浅层学习是接受信息的过程，记忆时间比较短. 深度学习是在理解的基础上加入自身的判断、归纳与整理等，从信息内在联系出发进行结构化的学习，记忆时间较长. 如表1所示，深度学习与浅层学习在记忆方式、知识体系、关注焦点、投入程度等方面均有所差别.

深度学习的特征

1. 深度学习具有批判性

学习者一旦处于深度学习阶层，就能批判性地理解所学知识，并以批判或怀疑的态度去审视学习材料，对知识形成客观的认识. 此过程中，学习者经历深入思考与分析，并基于理解的角度建构新知. 深度学习还能进行多学科知识的整合，让学生从多渠道批判性地认识并理解新知，在新旧知识的比较与分析中获得学习能力.

2. 深度学习更具迁移性

深度学习对学习者的要求较高，需要学习者在深刻理解情境的基础上准确判断关键性的学习内容，当遇到类似的情境需要触类旁通地去应用所学知识，这是知识的迁移过程. 同时，应用所学知识解决实际问题也是深度学习的特征之一，尤其是应用所学知识解决一些复杂的实际问题，体现学习者良好的迁移能力；而学习者对知识本质的掌握程度，决定其能解决多么复杂的实际问题.

3. 深度学习倡导主动性

深度学习是为了满足学生自身发展，主动掌握知识与技能的学习过程，而浅层学习只是被动地接受，完成教师所布置的教学任务. 随着知识的不断更新，想要保持强劲的竞争力，终身学习是唯一途径. 因此，深度学习是主动地学习，体现了学习的深度、广度与关联度.

深度学习的实施措施

1. 教学预评估

（1）学生的认知起点

学生在本节课学习之前接触过椭圆的概念、性质、标准方程、实际应用等内容，对解析几何也有了较为清晰的认识，因此本节课可应用类比法实施教学，让学生通过对椭圆学习方法的回顾，将研究过程迁移到双曲线中来.

（2）教学成效预估

双曲线的学习，能让学生充分了解双曲线的形成背景和形成过程，理解标准方程中系数的实际含义，同时提炼各种数学思想方法，理解双曲线的性质、离心率、渐近线的几何内涵，会应用相应知识解决问题.

2. 教学简录

（1）问题导学

问题1 巴西利亚大教堂的轴截面图的形状是什么样的？

问题2 回顾椭圆的定义，说说它有哪些限制条件.

问题3 若将椭圆定义里的“距离之和”替换为“距离之差”可获得怎样的轨迹图？

设计意图 引导学生从感性的角度出发回顾旧知，替换几何条件，将注意力投入思考状态.

（2）任务驱动

任务设计：要求学生取出课前准备好的纸板与拉链，拉开拉链，并在拉链的两侧各选一个点（两点不对称），把所选择的两点固定在纸板上一条直线的两个位置，将笔套在拉链拉头处画曲线，而后调换拉链长短的两头，同样再画出一条曲线，辨别这两条曲线的轨迹.

设计意图 实践操作，一方面可激发学生的学习兴趣与探索欲，另一方面可让学生在手脑并用中发现知识的形成过程，提高对知识的理解程度. 此过程，可增强学生对双曲线条件的理解.

（3）类比迁移

任务2 要求学生类比椭圆的定义，自主给双曲线下定义，并说说双曲线存在哪些限制条件.

任务3 要求学生自主探索2a=2c，2a>2c，2a=0三种情况下的轨迹.

设计意图 这三个任务的主要目的在于帮助学生更好地实现知识的类比迁移，其中任务1从高中生的实际认知水平出发，引导他们将注意力集中在“距离之差”（问题导学已提及）中，让学生自主发现形成双曲线的条件是在“距离之差”上添加绝对值.

（4）合理建构

任务4 要求学生从双曲线的定义出发，与求椭圆标准方程的建系、设点、列式化简等进行类比，推导出双曲线的标准方程，并在自主建构中设定未知参量，形成结论.

任务5 要求学生在自主思考的基础上合作交流，探讨不同的建系方法与解题方法，将自己的想法与同伴分享，在班级中展示交流结果后及时进行评价；师生共同探索双曲线位于x轴、y轴上的标准方程，以及方程中a，b，c所蕴含的意义.

设计意图 深度学习的目的在于提升学生的自主学习能力与探索精神，让学生形成良好的思维品质. 任务1要求学生能在自身已有的知识和经验上建构新知，这是促进学生进一步掌握标准方程的推导方法的基础，亦是促进学生全面发展的关键. 任务2的合作交流的开展，主要是为了给学生提供探索与展示的空间，补充双曲线方程的推导方式，以进一步拓展学生的思维.

（5）例题讲解，变式拓展

变式题2：把例1中的双曲线方程的a，b，c及焦点坐标写出来.

设计意图 设置由浅入深的问题，意在引导学生通过对双曲线方程中a，b，c的理解来发现双曲线位于坐标系中的位置.

设计意图 设置此例题及其变式题意在巩固学生对a，b同号的理解，并厘清焦点位于x轴、y轴上的双曲线之间的差别.

例3？摇？摇已知双曲线经过点P（－3，2）与Q（－6，－7），写出该双曲线的标准方程.

变式题：已知双曲线的焦点为（0，－6），（0，6），且过点A（2，－5），写出该双曲线的方程.

设计意图 设置例3及其变式题意在培养学生应用定义法、代入法等求解双曲线的标准方程；设置例4意在深化学生对“双曲线上任意一点到两定点的距离之差的绝对值是定值2a”的理解，变式题的应用让学生再次感知双曲线上一点到焦点的距离的最小值的限制条件，这可提升学生的数学严谨性与科学精神，避免后续在解题中出错.

（6）总结提升

要求学生自主回顾本节课学了些什么，应用了哪些学习方法、数学思想方法等，尝试用思维导图来总结本节课的知识结构.

教学思考

1. 深度学习需要批判性地应用理科思维

理科思维是从数据、逻辑推理等方面看待世界并解决实际问题的思维方式，更具理性特征，其核心是对知识进行量化与评估，通过对问题的综合考量做出决定. 如本节课的教学，教师通过数形结合思想、类比思想、建模思想等的应用，让学生在一次次的思维点拨中获得知识本质，形成良好的逻辑推理能力.

值得注意的是，部分教师更注重结果，对于探究过程没有过多要求，但深度学习需要弄清知识的来龙去脉、问题的源头与解题思路等. 本节课，教师带领学生从椭圆开始，通过类比分析获得双曲线的标准方程，学生由于亲历知识形成与发展的过程，因而记忆更加深刻，应用也更加灵活. 因此，教师应批判性地应用理科思维引导学生进行深度学习，应注重过程性教学，让学生在亲历知识的发展中获得深刻体验，形成触类旁通的能力.

2. 深度学习促进数学思想方法的提炼

深度学习包含数学思想方法的提炼与规律的总结等，这些都蕴含在知识的合情推理过程中，是数学的灵魂. 教师在授课时，不仅要关注知识与技能的传授，还要注重学生能力的培养，让学生从真正意义上脱离“题海战术”，获得正迁移知识的能力，这也是“减负增效”，提升学生数学学科核心素养的重要途径.

本节课，在教师的引导下，学生不仅亲历了归纳推理的过程，还提炼了数形结合思想、类比思想等，这是促进学生能力升华，获得良好的学习方法的关键.

3.深度学习有利于学生掌握数学知识本质

数学是一门研究事物数量关系与空间形式的学科，所有的符号与规律都源于人为的归纳与总结. 深度学习不仅能让学生体验到数学学科严谨、抽象等特征，还能让学生从发展中探寻出一些解题通法，从而提高学生的数学能力. 如本节课的教学，学生在深度学习中深刻掌握了双曲线的标准方程，后续遇到问题解决时，方法能手到擒来.

总之，深度学习是一种深入思维层面的学习方式，超越了具体的数学知识与技能，是一种从具体推广到一般的方法，它能让学生从真正意义上成为学习的主人，是促进学生形成终身可持续发展能力的关键.

参考文献：

［1］ 何玲，黎家厚. 促进学生深度学习［J］. 现代教学，2005（05）：29-30.