新课标下高二学生数列原理应用水平测试量表的编制与研究

［摘  要］ 基于新课标对数列内容的学习要求，以数学课程标准、SOLO理论和数学原理学习理论等为依据，采用定性研究与定量研究相结合的方法，制定衡量学生数列原理应用水平的研究框架，同时渗透考查学生对数列与函数之间的关系的理解，编制学生数列原理应用水平测试量表． 根据调研结果分析学生在数列原理应用存在的主要弱势，制定一个划分学生数列原理应用水平的参考标准.

［关键词］ 原理应用；数列；水平；测试；量表

作者简介：沈源钦（1988—），硕士研究生，中学一级教师，从事高中数学教学工作和教学测量研究，现任广州市高三数学中心组成员，曾获得全国青年教师优质课三等奖、广东省说课特等奖，广东省省级精品课、华南师大中小学联盟新课标教学设计一等奖等荣誉.

■ 绪言

2017年，教育部颁布《普通高中数学课程标准（2017年版）》，提出六大数学学科核心素养——数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析. 这六大数学学科核心素养既相互独立，又相互交融，形成一个有机整体，比如在数学公式的应用过程中，主要凸显逻辑推理和数学运算这两大核心素养［1］.

本研究选取高二年级学生作为研究对象，选取《普通高中教科书·数学·选择性必修第二册（人教A版）》中的数列内容为载体，结合数学课程标准、SOLO理论和数学原理学习理论等，采用定性研究与定量研究相结合的方法，尝试对数列原理系统作出一个比较合理的界定，提出衡量学生数列原理应用水平的研究框架，编制学生数列原理应用水平测试量表，并给出一个划分学生数列原理应用水平的参考标准，以期为一线数学教师教学提供参考，为培养或诊断学生数学学科核心素养的研究抛砖引玉.

■ 数列原理系统的界定

人们把在认识世界、发现各种事物的内在联系的基础上得到的计算公式、法则、定理、定律等叫做规则，或统称为原理. 加涅认为定义性概念也是一种特殊的规则［2］. 因此，本研究将定义式概念、公式、法则、定理、定律等界定为原理系统.

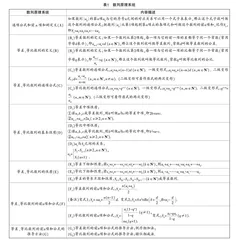
本研究将通项公式和前n项和的定义（A），等差、等比数列的定义（B），等差、等比数列的通项公式（C），等差、等比数列的基本性质（D），等差、等比数列的性质（E），等差、等比数列的前n项和公式（F），等差、等比数列的前n项和公式的推导方法（G），统称为数列原理系统（如表1所示）［3］. 数列原理应用主要是指利用数列定义、公式、性质等进行数值计算和数列公式应用变形.

■ 测试量表的编制

1. 量表的初始框架［4］［5］

《普通高中数学课程标准（2017年版）》将逻辑推理、数学运算素养水平均划分为三个层次，分别对应着在熟悉的情境、关联的情境、综合的情境中的逻辑关系推理和演绎推理. 将以上素养水平划分的指导性进一步转化为可操性，本研究结合SOLO理论关于单点结构、多点结构、关联结构的分类，按照完成应用任务所需要的数列原理的次数把数列原理应用划分为四个层次：第一个应用层次是指一次数列原理的简单应用，第二个应用层次是指两次数列原理的综合应用，第三个应用层次是指三次数列原理的综合应用，第四个应用层次是指多次（三次以上）数列原理的综合应用.

何小亚教授指出，数学原理学习可以分成四种水平：言语连锁学习水平、正向产生式水平（正用水平）、逆向产生式水平（逆用水平）、变形产生式水平（变形使用水平）. 同时考虑到数列公式包括原式、一级变形式、二级变形式（可看作原式的两次变形），以及与函数的联系，笔者把每一层次的测试题按照数列原理的正用、一次变形使用和多次变形使用分为三个难度等级（分别为一级、二级和三级），并适当加入函数观点进行检测. 其中，一级难度是指完成应用任务只需要正用数列原理；二级难度是指完成应用任务需要一次变形使用数列原理；三级难度是指完成应用任务需要两次或以上变形使用数列原理.变形使用包含数列一级变形式和二级变形式混合使用的情形.从而确定了一个比较合理的量表框架，每一应用层次的具体情况如表2所示.

2. 评价指标［4］［5］

曹才翰、章建跃教授将数学技能的行为指标分成四个：准确性、速度、协调性、自动化. 其中，准确性和速度是比较容易通过测试制定量化的标准的，而且这两个指标体现了运算技能教学中最基本的要求.因此，本研究选取准确性和速度作为评价学生数列原理应用技能的两个量化的指标.借鉴何小亚、植美贤老师的经验，以学生在限定时间内正确运用数列原理次数的情况来统计学生原理应用的速度，以学生正确完成题数的情况来统计学生运算的准确性.

3. 测试量表

何小亚、植美贤老师提出，测试量表的形成主要经历四个阶段：第一阶段是根据研究的框架，初选出测试题；第二阶段是征询专家意见，筛选和修改测试题；第三阶段是广泛征求专家教授和一线教师的意见，精选测试题；第四阶段是试测、修改，形成最终的测试量表，其结构如表3所示.

4. 量表的效度和信度分析

（1）效度分析.

参考华东师范大学出版的《教育测量与评价》关于内容效度的量化分析方法，考察题目实际测到的内容与欲测到的内容之间的相关程度如何，并且用四点量表表示. 该方法要求专家在仔细审阅测验目标的基础上，独立对测验的每一个题目作出判断：相关程度的大小. 四点量表为：“1”表示完全无关，“2”表示有点相关，“3”表示相关较密切，“4”表示完全相关.前两者为弱相关，后两者为强相关.当两位专家都完成了此项工作后，即可形成表4.

表4中的D表示两位专家都判定为强相关的题目数；A表示两位专家都判定为弱相关的题目数；B，C表示一位专家判定为强相关、另一位专家判定为弱相关的题目数. 这样，内容效度系数就可以用公式表示为：内容效度系数=.

根据上述原理，本研究专门对测试题的内容效度进行了量化分析. 为此，编制了“关于数列原理应用水平测试量表的调查问卷”，一共征求了10位专家的意见. 通过计算得出，本测试题的内容效度系数为0.9512，可见本研究编制的数列原理应用水平测试量表具有较高的效度.

（2）信度分析［4］［5］.

参考华东师范大学出版的《教育测量与评价》，本研究采用重测复本信度，以广州市某学校高二年级的一个班的学生作为重测对象进行测试（相隔3周）.记录该班学生两次测试中正确应用数列原理的次数和正确完成的题数，将每一个学生的两次测试成绩进行一一对应配对，利用SPSS18.0统计软件计算两次测试中正确应用数列原理的次数和正确完成的题数的相关系数，结果分别为0.992和0.980（α均取0.01）. 可见，测试具有较高的信度.

■ 实施与测验结果

广州市A，B，C三个不同层次共6所学校的高二学生的测验结果如下：

（1）被试总体的正确题数和正确次数成绩都是大致呈正态分布.

（2）6个被试组的正确题数成绩划分为较高、中、较低三个层次；而正确次数划分为较高、较低两个层次.这样划分是具有统计学意义的.

（3）被试总体的正确次数与正确题数成绩之间存在显著的正相关关系.

■ 数列原理应用水平划分标准的制定

根据样本分析结果作为常模参照，结合中学数学教师的经验，找到了三个指标：平均线、合格线和优秀线. 其中，平均线反映被试总体的一般水平，合格线反映被试达到了最基本的要求，优秀线表明被试达到了优秀水平. 本研究对样本按70%合格率和10%的优秀率确定［4］［5］. 其中用B代表正确次数（最大值为51），T代表正确题数（最大值为20），如表5所示.

这个标准参照表的实用意义是：对凡是学完了数列原理的学生在任何时间用本测试问卷，用时50分钟进行测试，均可对他们的数列原理应用有一个合适的定位.如果达到了标准参照表的要求，教师可以放心地积极前进；如果还没有达到标准参照表的要求，教师就要采取一定的措施进行弥补.

■ 研究局限与展望

由于条件与能力有限，本研究仍存在很多不足. 其中，对数列原理应用层次的划分是一种纵向划分，能否从水平方向作出维度划分，或有没有更好的划分方法等还有待研究.

本研究的对象都是广州市的学生，还可以进一步做乡村地区高中生的数列原理应用水平与数列原理应用水平的对比研究.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］. 北京：人民教育出版社，2020.

［2］ 何小亚. 数学学与教的心理学（第二版）［M］. 广州：华南理工大学出版社，2016.

［3］ 人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心.普通高中教科书·数学·选择性必修第二册［M］. 北京：人民教育出版社，2020.

［4］ 何小亚，植美贤. 高一学生对数运算技能水平测试量表的编制与研究［J］. 数学教育学报，2011，20（05）：55-58.

［5］ 植美贤，何小亚. 高一年级对数运算技能水平测试量表的编制与研究［J］. 中国数学教育研究会2010年国际学术年会论文集，2010-06-25.