量感的认知模型建构研究

摘  要：认知模型作为刻画学生认知过程的理论框架，在预测和解释各种问题解决行为的信息处理、学习测评等方面起到至关重要的作用。量感是学生形成抽象能力和应用意识的经验基础，是数学思维的重要因子。通过梳理相关文献，提取量感的七个属性；依据人教版小学数学教材中量感相关主题的课程顺序，以及小学生认知发展规律与特点，初步建构量感的认知模型；运用专家指导的方法对初步确定的认知模型进行矫正，并通过解释结构模型和学生口语报告验证该认知模型的科学性。

关键词：认知模型；量感；认知诊断测评

现代化社会是数字驱动的社会，数字化时代对人才的要求越来越高，人们解决问题已不能单单从经验或直觉中提取策略

［1］，而是要求人们能够以量化的思维分析问题，用定量的方式解决问题。

量感的提出是现代化社会对人才培养的精细化要求。

在小学阶段，量感的培养是学生形成用定量方式解决问题思维的基础。认知模型作为一种理论框架，能精细地刻画知识内部结构，从而清晰地看出知识、技能等相关要素之间的关系，进而对学生的知识、技能等相关要素的掌握情况从微观层面加以详细描述。我们首先分析了量感的知识结构和认知过程等，然后尝试建构量感的认知模型，并通过解释结构模型和口语报告验证模型，试图为量感的认知诊断测评提供依据。

一、量感与认知模型的界定

（一）量感的界定

对于“量感”，概括起来可分为三类认识。

第一类，量感指的是学生在实际情境中主动地、自觉地理解和运用“量”的态度和意识。它是一种对“量”的直觉，对“量”的敏感性，对“量”的直接反映，指的是不使用测量工具对某个量的大小进行推断，或推断用某个单位表示的量与哪个实际物体的大小相吻合的一种感觉。［2］

第二类，量感来源于数量感，量感与数量感对立又统一。数量感去情境化分化为数感，强调抽象后的数值部分；加情境化分化为量感，强调具体化的物理意义。

［3］另外大卫·瓦格纳（David Wagner）等人认为，数量感是数字感发展的基础，数量感有两层含义：一是，对多少、大小的感觉；二是，对数量和量级的感觉。［4］

第三类，量感主要是一种心理感受，是一种对长度、质量、时间、面积、体积等可测量属性的感性认识，是一种由外而内、内化而成的感觉。［5］《义务教育数学课程标准（2022年版）》（以下简称“课标”）采用的就是此类定义，即量感主要指对事物的可测量属性以及大小关系的直观感知。［6］

（二）认知模型的界定

认知模型，最初源自计算机科学领域，是对人类解决问题和心理处理任务的一种模拟。从认知心理学的角度来看，是对学生解决问题的简化描述，可以表示为学习层次结构。

［7］在教育测量中，认知模型是解决问题的抽象，选择合适的粒度刻画任务，通过

对任务的解答情况来解释和预测学生在某一主题中的表现。［8］

总之，在教育研究中，认知模型是对认知属性及属性结构关系的一种直观展现。它可以详细解读某一主题内部的属性结构，也可以刻画学生对某个主题的知识、技能等要素的掌握路径，进而为某一主题的认知诊断测评提供前提条件。本文所建构的认知模型主要是指学生解决量感问题的思维过程模型，是基于认知心理学所建构的解决量感问题的心理加工机制模型

［9］。

二、量感的认知模型建构

（一）量感的认知属性

认知属性是指学生正确完成任务所需的知识、技能、策略等，它是对学生问题解决心理内部加工过程的一种描述。量感的认知属性是对学生解决量感问题时心理内部加工过程的描述。基于对量感认知属性的界定，首先从已有的研究中得到量的测量判断、量的理性感知、量的单位转换等属性。［10］然后分析各国数学标准发现，在小学阶段与量感密切相关的测量主题中包括周长、面积、体积、容积等量的公式应用是小学生解决量感问题时重要的组成部分

［11-13］

。基于此，提取量感的一个属性量的公式应用，又通过对人教版小学数学一到六年级教材的分析发现，每个量的学习都会涉及量的比较，包括直接比较和间接比较。另外，教材中各种量的经典习题、例题主要是对生活实际中量感问题的描述，但是这类问题通常比较复杂，需要运用推理、转换等方法进行解决，我们把涉及解决这类问题所需的知识、技能等

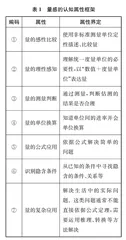
要素的描述称为量的复杂应用。最后，参考康春花、辛涛等人编制的“小学数学应用题”认知属性框架中的观点，“解决数学应用题时需要识别隐含条件”［14］。我们认为，解决量感应用问题时同样需要识别隐含条件。综上，得到量感的认知属性框架（详见下页表1 ）。

（二）量感认知属性的关系

雷顿（Leighton）等人认为，认知属性不是独立操作的，而是从属于一个相互关联的网络

；认知属性之间可能存在一定的心理顺序、逻辑顺序或层级关系，即认知模型就是用来表征相关任务的属性关系图。［15］量感认知属性关系的初步

搭建，主要依据课标和人教版小学数学教材中量感相关主题的课程顺序、小学生认知发展规律与特点以及四国课标中

对量感密切相关主题（测量）的分析。于是，我们初步绘制了量感的属性结构关系图（如图1所示）。

图1

三、量感认知模型的矫正与验证

（一）量感认知模型的矫正

在认知模型的建构中，前提是确保模型中的属性和属性之间的关系能够准确且有效地反映出学生在答题时潜在的认知过程。准确的认知模型才能为推断学生的学习状况提供可靠的依据。因此，对初步提取的属性以及绘制的属性关系图，邀请八位专家进行

指导矫正。其中，两位是高级小学数学教师，两位是市级小学数学教研员，他们都有着丰富的教学经验和对学生的了解；两位是教育统计与测评领域的教授，专门研究数学课程与教学、教育测评，可以从理论层面

对量感的认知模型进行考察；两位是研究小学数学方向的研究生，能够从小学生的角度审视认知模型。通过公开问卷调查，邀请每个专家对7个属性的重要性进行判定（每个属性的重要性为1—5分，总分为35分），并绘制属性结构关系图。专家的判定结果详见下页表2。

我们把每个专家对属性的重要性判定总分超过满分的三分之二的属性确定为量感较重要的属性。由此可知，初步提取的7个属性皆为量感较重要的属性。通过专家的结构图与初步绘制的属性关系图的比较，我们可以得到矫正后的量感认知模型：如下页图2所示，①是掌握②的先决条件，②是掌握

③

的先决条件，③是掌握④和⑤的先决条件，④和⑤是掌握⑥的先决条件，⑥是掌握⑦的先决条件。

属性层级关系体现的是个体心理加工过程中各认知属性掌握的难易程度和认知发展

的先后顺序。［16］比如，量的复杂应用往往比识别隐含条件更难，换句话说，个体需要在熟练识别隐含条件的基础上才可掌握量的复杂应用。

（二）量感认知模型的验证

1.基于解释结构模型的验证

解释结构模型（ISM）是将人们在处理复杂问题时遇到的困难以一种清晰明了的方式

解释为造成困难的因素以及各因素之间的关系，并以一个明确清晰的结构表达。［17］在ISM中，确定了与问题相关的因素之后，为了分析因素之间的关系，需要建立一种上下文关系，这种上下文关系可以表达为一个因素影响了另一个因素或者导致另一个因素怎么样。因此，在ISM中因素之间存在一种因果关系，这种因果关系的判定通常由领域专家对因素两两之间进行判定，进而形成结构自交矩阵（Structural Self-interaction Matrix，简称SSIM）。以量的感性比较（①）和量的理性感知（②）为例，从ISM的角度分析量感属性层级关系。学生通过身体的某一部位量一量桌子有多高、掂一掂书包有多重或者借助第三方工具比较其他两个物体的长度、质量等，都是学生基于自身的经验来感性比较某一个量。在这个过程中，每个学生使用的测量单位不同，导致测得的结果并不一致。如何使同一个量的测量结果一致？学生只有理解了统一度量单位，并用统一的度量单位测同一个量才可以得到一致的测量结果，这个结果可以用“数字+度量单位”进行表达。因此，①导致②的产生，①和②之间构成因果关系。总的来看，量感认知模型以一个明确清晰可操作化的方式表达出来其建构思想与ISM的思想一致，即从ISM来看，建构的量感认知模型较为合理。

2.基于口语报告的验证

口语报告法指的是被试在测试中将自己的解题思维过程以口头报告的形式表达出来，测试者将这一过程记录下来并加以分析。［18］

我们从某小学六年级某个班级中随机选取2名学生，一名成绩较好，一名成绩中等。要求学生在无干预的情况下解答测试题，同时以特定的数学语言说出自己头脑中进行的思维活动（即时性口语报告）。我们对学生作答表现的情况做记录，并全程录音。

测试材料由出声思维的测试题、学生作答所需文具和录音笔构成。

我们依据所界定的认知属性及其层级关系选取国际数学和科学研究趋势（TIMSS）中的测试题，稍加修改，最终形成如下测试题：

测试题  赖安正在把书装进一个矩形的盒子里。如图3所示，书厚6厘

米、宽15厘米、长20厘米。盒子从里面量高是2分米、宽是3分米、长是3.6分米。这个矩形盒子最多能装下多少本这样的书？

第一位学生的口述作答思维过程如下：

（1）实际涉及容积与体积之间的比较，预估最多可装10本书。

（2）统一单位。

（3）2分米=20厘米，3分米=30厘米，3.6分米=36厘米。

（4）书可以看作长方体，书的厚度是长方体的高，书的长是长方体的长，书的宽是长方体的宽，矩形盒子可以看作一个长方体的容器。

（5）体积公式为长×宽×高，容积同体积一样。

（6）最多装下多少本书，实际在计算矩形盒子最多能容纳下多少本这样的书，首先应求得一本书的体积和盒子的容积，书的体积=20×15×6=1800（cm3） ，矩形盒子的容积=20×30×36=21600（cm3）。

（7）矩形盒子的容积除以一本书的体积，21600÷1800=12（本），矩形盒子最多可装12本书。

第二名学生的口述作答思维过程如下：

（1）比较矩形盒子的容积与能装下最多书的体积，统一单位。

（2）估计能装十多本书。

（3）2分米=20厘米，3分米=30厘米，3.6分米=36厘米。

（4）体积公式为长×宽×高，书的体积=6×15×20=1800（cm3），盒子容积=20×30×36=21600（cm3）。

（5）21600÷1800=12（本）。

可以看到，两名学生首先提出比较盒子容积与一本书的体积（①），接着提出要统一单位（②）；第二名学生估测能装十多本书；然后，提出单位换算（④），并直接应用体积公式求得一本书的体积和矩形盒子的容积（⑤）；最后，识别出隐含的关系即一个矩形盒子最多能装下多少本这样的书，可以用矩形盒子的容积除以一本书的体积（⑥⑦）。可见，学生的思维作答过程与量感认知模型图中的属性层级关系较一致。因此，从学生的口语报告来看，建构的认知模型大致符合学生的认知过程。

数学教学的根本任务就是要培养学生良好的数学认知结构，以满足后续学习的需要，最终提高学生的问题解决能力。在教学实践中，教师要培养学生良好的数学认知结构，首要的是了解学生原有的认知结构，知道学生原有的认知结构存在什么优点和缺点，这样教师才能够知道选择教什么和怎样教。［19］量感认知模型