数学史料“古法今用”教学实践

数学史料“古法今用”教学实践0

摘要：现代的标准化乘法竖式是一种概括的简写形式，缺少了一部分过程，掩盖了进位的含义，导致学生无法全面地思考“先乘再加”的计算过程，不知如何操作进位数字。对此，在学生初步掌握乘法笔算的基础上，设计一节拓展课，以画线乘法、格子乘法为主要学习材料，同时介绍

视窗法、筹算法和叠果法等方法，引导学生感悟它们背后的“通理通法”。这样的教学，突破了学习的难点，重燃了学生的兴趣。

关键词：小学数学；数学史；多位数乘一位数；算理；算法

一、课前思考

多位数乘一位数是理解与掌握整数、小数乘法笔算的关键，是学生真正理解乘法笔算算理、归纳掌握算法的载体。多位数乘一位数的笔算中，（连续）进位最容易出错。究其原因，现代的标准化乘法竖式是一种概括的简写形式，缺少了一部分过程，掩盖了进位的含义，导致学生无法全面地思考“先乘再加”的计算过程，不知如何操作进位数字。如何将现代乘法竖式中的算理进一步可视化，帮助学生实现理解呢？在学生初步掌握乘法笔算的基础上，我们设计了本节拓展课，融入古代乘法计算方法，引导学生思考各种不同方法中的“通理通法”。

通过研读有关乘法笔算的数学史料，我们决定以画线乘法、格子乘法为主要学习材料，同时介绍视窗法、筹算法和叠果法等方法，引导学生感悟它们背后的“通理通法”。有别于古代算法出现的历史序，本节课按照学生经验和思维水平的认知序进行设计。

学生在读懂画线乘法中“线条代表什么”“积是怎样算得的”等关键问题的过程中，能够较为直观地体会“通理通法”：先将多位数按数位分解，再分别与一位数相乘，最后将各个数位上的计算结果合起来。

格子乘法在乘法笔算的历史中影响深远，传至中国时被称为“铺地锦”。其结构规整，在格子中保留了计算的全过程，进位数字清晰可见。与现代乘法竖式中标识进位的“小数字”相比，格子乘法在计算时更容易看清进位数字，不容易忘记进位，同时有助于检验计算步骤。

视窗法与前两者相同，具有可视化的优点。其中的“视窗”部分，将现代乘法竖式被压缩、省略的各步计算过程展开体现，化解了进位的难点。

本节课引导学生关注不同算法之间的沟通与联系，感受“存异”，更注重“求同”，即无论哪种方法，都要经历“分—算—合”的过程。通过可视化手段，聚焦古代算法与现代乘法竖式的“通理通法”，促进学生理解“将因数按数位分解”“满几十要向高一位进几”等算理，感悟背后的十进位值制记（计）数思想。

《义务教育数学课程标准（2022年版）》要求，课程内容选择关注数学文化，继承和弘扬中华优秀传统文化。数学史是数学学习厚实的理解背景，将数学史融入数学教学，能还原被

压缩、省略的丰富细节，能开拓一条深度理解的学习路径。引入古代乘法笔算方法，架起古代算法与现代乘法竖式之间的桥梁，呈现乘法竖式发展变化的数学文化脉络，能让学生体会到不同时代（地区）乘法笔算的算理本质是一致的，只不过算法形式不同。

总之，本节课旨在创造“算理可视化、算法一致性”的学习情境，促进学生真正理解乘法笔算的算理与算法，反思解决竖式计算中出现的“进位、遇0易错”的真问题。

二、教学实施

（一）复习回顾，以史激知

师关于乘法笔算，你知道多少呢？我们先复习一下乘法笔算，请你用竖式计算42×6，写到你的学习单上。

（学生用竖式计算，教师巡视。）

生 42×6，先算个位，2×6=12，进“1”写“2”；再算十位，4×6=24，24加进位的1等于25，进“2”写“5”；然后在百位添上进位的2，就是252。

师从个位算起，老师看到很多同学养成了好的习惯：标上数位。

生（齐）个位、十位、百位。

师（板书数位）最后还要记得将结果写到横式上。（稍停）同学们，你们知道古人是怎样计算乘法的吗？今天我们一起来了解一下。

（二）读懂古代算法，提炼“通理通法”

1.读懂画线乘法

师在古代，有一种乘法计算方法叫作画线乘法。听听它的名字，你觉得它会是什么样子的呢？

生画线乘法肯定有线条。

师得画线。真好！还有什么你想知道的？

生我想知道画线乘法到底怎么画线才能算出乘法来。

（不少学生表示同意。）

师线是怎么画的？线代表什么？真会思考！还想知道什么？

生我想到，画线乘法应该不是只有线，还有别的东西。

（一些学生陷入了更深入的思考。）

师就以42×6为例。

（教师逐步播放画线乘法计算42×6的动画过程。学生在观看时发出“嗯？”“咦？”和“哦！”的声音。）

师好像有同学看懂了，谁来说说？

生我的理解是，图中每一个交叉的点就是一个数。

（学生有的点头，有的皱眉。）

生我发现上面有4条横线，下面有2条横线，是不是就代表42呢？

（学生有的点头，有的思考。）

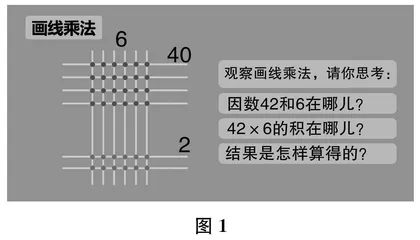
师看来，要想看懂画线乘法，就得搞懂：因数42和6在哪儿？积又藏在哪儿？是怎么算得结果的？

（课件出示图1。）

（越来越多的学生举手。结合图1中的计算过程以及教师提出的问题，学生基本理解了画线乘法的计算过程。）

师你们觉得古人这个画线乘法怎么样？谁来评价一下？

生我觉得还行，就是没有现代的竖式简单，有点麻烦。

师哪里麻烦？

生得（ｄěｉ）数（shǔ），还得画线。先得画线来表示因数，还得数点来得到结果。

师我们感觉到了，画线乘法还是挺——

生智慧的。

师但又有点麻烦。

生如果多画或少画了一条线，就错了。

师画线乘法是古人计算乘法的方法之一。其中，横着的线条表示第1个因数，它会把十位、个位分开；竖着的线条表示第2个因数；积就藏在横线与竖线交叉的那些点上……

2.读懂格子乘法

师刚才，有同学觉得画线乘法还是很麻烦，而且有易错的地方。古人的智慧也在发展，于是后来出现了格子乘法。想象一下，格子乘法会是什么样子的呢？

生格子乘法，我觉得，得有格子，但也不可能只有格子吧？

（多数学生点头。教师逐步播放格子乘法的计算过程。学生观看。）

师你看懂格子乘法了吗？如果你有想法了，可以写在学习单上，或者先跟同桌讨论讨论。

（学生热烈讨论后，教师请一位学生到讲台上展示交流。）

生（出示图2）上面的42是第一个因数，右边的6是第二个因数；2×6=12，4×6=24；12的“1”和“2”中间被一条线分开，上面是十位，下面是个位；24也被分开，“2”在百位上，“4”在十位上。于是，百位直接写上2，十位4+1=5，个位直接写上2，左边和下面连起来的252就是积。

（学生自发鼓掌。）

师要读懂格子乘法，首先要先找到因数。那么，格子里是什么？

生格子里是因数乘因数的过程。

师这个格子是怎样分的？

生按照数位分的。

师最右边是个位，中间是十位，最左边是百位。那么，积是怎么得到的呢？

（学生回答，教师板书。）

师总结一下，格子乘法先算个位（板书：2×6=12），再算十位（板书：40×6=240），最后把这两步的结果加起来

（指着刚才的板书）。格子乘法给你什么样的印象？

生我觉得画线乘法线太多了，还得数，格子乘法简洁了很多！

生（之前提出画线乘法易错的学生）格子乘法更不容易出错：十位上有时有进上来的数，要记得把它加起来。

3.读懂视窗法

师我们已经有两个研究古代乘法的经验了。古人的智慧真

的很厉害！（课件出示“视窗法”的名称）关于视窗法，你有什么想说的？

生什么是视窗？

（教师逐步播放视窗法计算42×6的动画过程，画面定格在图3。）

生视窗法和我们现在的竖式真像啊！

生第一行的12是个位2×6的结果；第二行的24是十位4×6的结果，表示24个十。

生 2×6=12；40×6=240，所以“2”写在了百位，“4”写在了十位。

师现在请你跟小组同学再交流一下视窗法的计算思路。

（学生交流。）

师视窗法写出了计算过程的每一步（写出的计算过程称作视窗），并且将每一步所得的积对齐写在各个数位上，最后把两步的结果加起来。

（三）对比沟通，理解算理

师虽然我们以前没有接触过古人的算法，但是经过深入思考，慢慢地了解了很多。现在请你思考：古代的算法和现代的有什么相似之处呢？

生画线乘法有点麻烦。比如，9×99，得画多少条线啊！而且，画线乘法需要分开点儿画，要是不分开，靠得太紧，就分不清数位了。如果是更多位数，那么进位时，还得列好多个式子！

生画线乘法在加的时候，遇到进位容易出错。

师画线乘法要求画得清楚，最后加的时候，进位易错。你给同学们很大的启发！谁还愿意再说一说？

生我发现，这些古代算法最后都要把个、十、百位上的数合起来。

师同学们又找到了特别重要的一点：不管是古代的还是现代的，乘法笔算过程中都有一个重要步骤：将各个数位上计算的结果合起来。

那么在合起来之前，还有共同点吗？

（学生思考后，意识到：都是“先分再算”。）

师你们找到了它们的共同点：现代的算法和古代的算法其实都经历了“先分，再算，最后合”的过程。我们把它称作“通法”。（稍停）还有共同之处吗？

生我发现，它们的数位一直没变，都是个、十、百（位）。

师这一点很关键。在各个算法中，我们都是按照个位、十位、百位等数位进行计算的。这背后藏着一件重要的事：我们都是按照个、十、百等数位对因数进行分解的。这说明计算的道理藏在计数的方法中：我们按不同的计数单位对应不同的数位来计数，所以要按不同的计数单位，即不同的数位来分步计算。（稍停）

那么，你们更喜欢哪种计算乘法的方法呢？

（学生纷纷表达观点，喜欢各种方法的都有。）

师看来，大家被古代的算法深深地吸引了，因为，它们形式多样，同时背后的道理是一样的。相比之下，我们的竖式计算过程更为简洁。

（四）温故知新，灵活运用

1.拓宽视野

师今天，大家认识了古代的三种乘法算法。其实，古代的乘法算法还有很多。比方说中国古代的算筹法：古人拿着算筹这种类似小棒的工具，每次计算时都要摆一摆、数一数。