推理意识的培养要做到“三全”

摘 要：发展推理意识是培养推理能力的经验基础，是小学阶段提升数学思维的重要目标。小学数学教学中，学生推理意识的培养要做到“三全”：“全领域”覆盖，即利用好教材中各领域适合培养学生推理意识的教学内容；“全过程”经历，即引导学生充分体验推理的过程，帮助学生对推理过程及其意义形成初步的感悟；“全方位”理解，即让学生逐步养成讲理、明理的思维习惯，学会有理有据地表达交流。

关键词：小学数学；推理意识；合情推理；演绎推理；推理表达

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）明确提出了“三会”数学核心素养，其中的“会用数学的思维思考现实世界”相对侧重的是推理。由此，关于推理能力的发展路径清晰明了地展现出来：从小学阶段的推理意识，到初中阶段的推理能力，再到高中阶段的逻辑推理，循序渐进，一脉相承。发展推理意识是培养推理能力的经验基础，是小学阶段提升数学思维的重要目标。笔者以为，小学数学教学中，学生推理意识的培养要做到“三全”：“全领域”覆盖，即利用好教材中各领域适合培养学生推理意识的教学内容；“全过程”经历，即引导学生充分体验推理的过程，帮助学生对推理的过程及其意义形成初步的感悟；“全方位”理解，即让学生逐步养成讲理、明理的思维习惯，学会有理有据地表达交流。

一、“全领域”覆盖

综观现行小学数学教材，推理贯穿整个小学数学学习内容，涵盖“数与代数”“图形与几何”“统计与概率”“综合与实践”四大领域。小学数学教材中的推理不同于具体数学知识点，它是隐性的、缄默的，在各大领域的存在形式和发展要求也不尽相同。因此，常常会被教师忽视。基于新课标要求，教师应认真审视教材，在核心素养导向下对教材进行实践性解读，尝试结合四大领域的特点梳理素材。

新课标在“数与代数”领域特别强调算理与运算的一致性，反映出对代数推理的重视。在这个领域，数的认识、数系发展规律的探索和各种运算法则、运算律的发现与总结等，都是发展推理意识的有效依托。比如：在学习整数加减法的基础上，让学生合乎逻辑地推出“小数、分数加减法其实也是计数单位的累加”；基于加法的数量关系，引导学生解释减法是加法的逆运算，乘法是加法的简便运算，除法是乘法的逆运算，彻底打通四大运算的脉络；等等。

“图形与几何”领域的推理主要体现为直观推理。在图形的认识、测量、运动和位置确定中，概括图形的特征、归纳图形的要素、推导图形的计算公式等，都是发展推理意识的有力素材。比如：学生根据前面、右面、上面看到的“三视图”，在头脑中想象、推理、调整、筛选，逐步确定最终的图形，从二维到三维的进阶也是推理水平的一次飞跃；在学习长方形的面积计算时，学生从直观地数小方块，到发现小方块的个数与长、宽的联系，再到提出猜想，最后到说理推导；之后，以长方形的面积计算为起点，整个图形领域的推导都可以追溯源头，一次次经历的过程就是推理意识萌芽并生长的过程。

“统计与概率”领域的统计推理也是数学推理的一种。统计推理的分析对象是数据，目的是对未知事件作出有证据的、有说服力的预测。虽然统计推理是一个相对主观的推断，但是同样需要有理有据地思考，能有效地体现学生的思维水平。比如：利用折线统计图反映某儿童6—12岁的身高变化情况，并对该儿童13岁的身高作出合理的预测；在反复的摸球活动中，根据摸出球的颜色，预估下一次的摸球情况或猜测口袋中球的颜色；等等。统计推理与其他的数学推理虽然不太一样，但其核心也是培养数学思维，教育意义不容小觑。

“综合与实践”领域的推理主要指学生通过观察，利用生活中的现象、事件，发现规律，作出推理，更多地体现为各种推理的综合运用，以及在生活中的实际应用，是一种生活实践推理。比如：《数字与信息》这节课中，学生根据身份证上数字编码的规律，推理发现出生年月，判断性别；根据某学生的学籍号，判断该学生的入学年份，推算出该学生现在就读的年级；等等。

在四大领域中，发展推理意识的有效素材和合理依托并不少，教师要进一步明确新课标背景下推理意识的内涵，努力挖掘与开发，做到“全领域”覆盖。

二、“全过程”经历

（一）充分体验合情推理

合情推理是从特殊到一般的推理过程，主要通过归纳和类比获得猜想，再用举例验证、生活经验、直观图形等多种方式加以解释，进而得到结论。

合情推理是引导学生进行数学发现的重要途径，关乎学生思维能力和创新能力的培养。教师可通过设计丰富的数学活动，鼓励学生经历“猜想—验证”的过程，凸显完整性、追求理解性，帮助学生积累活动经验，发展推理意识。

以苏教版小学数学三年级下册《有趣的乘法》一课中的规律探索为例。

1.师生比赛，激发兴趣

首先，教师出示一组算式（14×16、22×28、77×73、55×55），师生比赛计算，教师以惊人的计算速度激发学生的好奇心，从而引导学生观察算式及结果的特点，开启探究之旅。

2.大胆猜想，验证完善

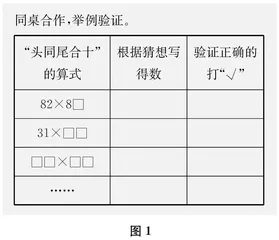
通过观察，学生发现算式的特点是“头同尾合十”，结果的规律是“积的末两位等于两个乘数个位上的数相乘，积的前面等于十位上的数乘比它大1的数”。但根据四个算式得到的规律仅仅是一个猜想，并不能说明具有普遍性，教师引导学生进行验证。而在验证59×51时，学生对结果产生了分歧，于是，教师引导学生进一步完善猜想：如果个位乘个位的结果是一位数，要在十位添“0”。完善后的猜想是否正确呢？教师再一次引导学生举例验证（如图1所示），进一步提升结论的可靠性。教师在教学中不急于得出结论，而是让学生充分经历“猜想—验证—发现反例—完善猜想—二次验证”的过程。

3.借助图形，直观明理

以上验证得到的规律，对于小学阶段的学生还不需要严格的推理证明，但教师可以用方块图解释规律背后的原因，借助直观推理探析规律的合理性，丰富学生的推理形式，提升学生的思维能力。比如，14×16=224，可以借助图2来帮助学生直观地明白规律背后的原理。

最后，教师带领学生完整回顾观察、猜想、验证、得出规律的全过程，帮助学生领会在变化中探寻不变、从特殊中归纳事物一般属性的方法，为以后的数学探究积累宝贵的合情推理经验。

上述教学案例主要是归纳推理的过程，教师在教学中还可以适时渗透类比推理的思维方式。例如，数的意义、读写、运算等，都可以进行类比推理的渗透教学，通过新旧知识之间的勾连，实现知识和方法的正迁移，促进知识结构化。

（二）适时尝试演绎推理

如果说合情推理注重探索发现，那么演绎推理则体现务实严谨。演绎推理是由一般到特殊的推理方式，通过演绎推理可以将合情推理得到的结论加以验证。演绎推理具有较高的抽象性和挑战性，很多时候小学生还不具备严密推理的能力。在实际教学中，教师在充分拓展合情推理空间的同时，可以选择合适的内容、合适的时机、合适的学段，尝试让学生经历演绎推理的全步骤，感悟严密性，逐渐完成从推理意识到推理能力的自然进阶。

例如，“3的倍数特征”是苏教版小学数学五年级下册的教学内容，教师通常会让学生经历“观察比较—提出猜想—举例验证—得出结论”的合情推理过程。在验证环节，有两种方式：一是再举一些例子看看是否符合特征，二是看看能否举出反例。然而，举再多的例子也只是合情推理。对此，在六年级总复习阶段，教师可以通过演绎推理的方式再次教学“3的倍数特征”，以打通小升初的隔断，让数学思维从浅表走向深刻。具体教学过程如下：

1.“为什么”问题驱动

临近毕业的六年级学生，对于“3的倍数特征是什么”熟记于心，但当被问到“为什么判断一个数是不是3的倍数，只要看各个位上数的和是不是3的倍数”时，学生陷入了沉思。于是，在探寻“为什么”的问题驱动下，教师带领学生开展深度探究。

2.“圈一圈”初探本质

教师引导学生进行有层次的直观操作，圈画表征，把握关键。首先从简单的两位数“21”圈起（如图3所示），再到三位数“134”（如图4所示），进而要求学生在头脑中分析四位数“1518”，引导学生循序渐进地看图说理、想图说理。教师指导学生根据直观操作和位值原理，明确每一个计数单位里都会有最大的3的倍数（如9、99、999等），于是只要考虑剩下的数的和是不是3的倍数即可。借助图形推理让学生对3的倍数特征有了更为直观清晰的理解，帮助学生向抽象的理性分析靠近了一大步。

3.“数与形”融合说理

直观操作演示为抽象推理提供了脚手架。教师可以引导学生将每一步的直观操作用形式化的推演表示出来，抽象的算式和直观的操作一一对应（如图5、图6所示），相辅相成。直观背景下的抽象推理促使学生的说理更为深刻。

4.“字母式”抽象进阶

形式化的推演还不是严格意义上的演绎推理，但已经初具演绎推理的模型。教师通过问题引发学生思维再次进阶：像“21”这样的两位数一共有90个，如果每一个数都要进行推理说明，一共要进行90次，能不能用一个推理过程来涵盖呢？此时，字母式恰到好处地“登场”，从两位数到三位数，学生尝试经历演绎推理的过程（如下页图7所示）。

小学生直接接触演绎推理是有难度的。这一案例选择在六年级总复习阶段实施，循序渐进，环环相扣，让学生自然而然地体验演绎推理的过程，思维在不经意间实现高层次进阶。从学生的课堂反馈来看，他们不仅做到了“知其所以然”，还感受到了用字母式进行演绎推理的严密、规范等优势，为初中进一步发展推理能力奠定了坚实的基础。

三、“全方位”理解

要真正理解（悟透）数学推理，除了需要经历观察、思考、操作、发现等数学活动，还需要把推理的过程和得出的结论用语言表达出来。清晰的数学表达是发展推理意识的一种外显形式，而推理意识的发展又伴随着数学表达的提升。发展推理意识和培养数学表达是相辅相成的，这恰恰也体现了数学核心素养是共为一体、互为支撑的。教学中，教师应有意识地鼓励学生清晰、完整地表达，让学生在有理有据的数学表达中，全方位地理解。

例如，第一学段教学“整十数乘一位数”时，教师不仅要关注20×3的计算结果，更要关注学生思考的过程。学生可以利用已有经验“20、40、60”数出来，也可以转化成“20+20+20”加出来，还可以借助方块学具推算出来。教学中，教师要引导学生多元化表征自己的思维过程，鼓励学生理解并表达“2个一乘3得6个一，2个十乘3得6个十”，体会知识之间的联系，感受计算本质的一致性。

又如，第二学段教学“三角形的分类”时，教师引导学生观察比较，发现异同，用简洁准确的数学语言进行概括表达。类似“直角三角形的另外两个角一定是锐角吗？”“一个三角形中可能有2个直角吗？”这样的问题，学生的回答不能仅仅停留在“一定”“不一定”或“可能”“不可能”上，教师要给学生充分交流表达的时间。学生可以结合三角形的内角和是180°，将前后知识贯通起来进行有理有据的解释，抑或结合画图、操作学具等方式形象直观地加以说明。在交流表达的过程中，学生深入理解知识本质，发展推理意识。

再如，第三学段教学“比的基本性质”时，教师引导学生对教材中的具体例子进行清晰的表达，如“比的前项乘4，后项也乘4，比值不变”“比的前项和后项同时乘10，比值不变”等。然后，教师引导学生勾连已经学过的“分数的基本性质”“商不变的规律”，用语言表达学过的知识，并说清前后知识之间的联系。最后，顺水推舟地概括归纳出“比的基本性质”。整个学习过程，在螺旋上升、准确合理的表达中水到渠成，在归纳推理和类比推理的交相呼应中画上句号。

推理是表达的前提，表达是推理的结果。在教学实践中，数学表达有“说”和“写”两种，教师应引导学生敢于表达、学会表达、善于表达，训练语言的准确性、简约性和逻辑性。同时，教师也要鼓励学生尝试用数学符号、数学图标等方式，合乎情理地表达。在形式多样的表达过程中，逐步发展推理意识，学会数学地思考。