基于计数单位,感悟数概念的一致性
作者: 陈辉英
【编者按】 强调一致性,而不是“各讲各的理”,从而让不同的数学内容形成整体,是《义务教育数学课程标准(2022年版)》修订时的指导思想之一。比如,“数与代数”领域强调基于计数单位的数的概念的一致性和数的运算的一致性,“图形与几何”领域则强调基于度量单位的“数学度量的一致性”。本期《专题研究》栏目刊发3篇相关研究文章。
摘 要:“感悟数的概念的一致性”,是《义务教育数学课程标准(2022年版)》对“数的认识”教学提出的新要求。数概念的一致性源于构建数概念的核心概念一致和数概念指向的核心素养一致。为帮助学生感悟数概念的一致性,教师需要整体分析“数的认识”内容,凸显计数单位的统领作用;引导学生充分经历数数和比较的过程,感受数是计数单位的累加,计数单位是数概念的共同本质。
关键词:小学数学;课标修订;数的认识;计数单位;一致性
强调“数的概念(本质上)的一致性”和“数的运算(本质上)的一致性”,是《义务教育数学课程标准(2022年版)》(以下简称“新课标”)相对于《义务教育数学课程标准(2011年版)》修订的五个要点之一。[1]其中,数概念的一致性是数的运算的一致性的基础。那么,在小学阶段“数与代数”领域“数的认识”内容(包括关于整数、分数、小数的认识的多个单元)的教学中,如何理解数概念的一致性?如何帮助学生感悟数概念的一致性?本文谈一谈笔者的思考与实践。
一、如何理解数概念的一致性
(一)数概念的一致性源于构建数概念的核心概念一致
新课标指出,小学阶段“数的认识”的教学,要让学生“在理解整数、小数、分数意义的同时,理解整数、小数、分数基于计数单位表达的一致性”[2]。从数概念的发展史看,记数制的发展过程就是计数单位的创造过程。[3]自然数是由“ 一(个)、十、百、千……”等计数单位累加得到的。首先由小到大“一个一个”地数(非进位制),接着“一组一组”地数(进位制),这个“一组”就是进位,是新的计数单位。分数和小数是数的认识的扩充。分数的扩充来自表达比1小的数量,需要对一个“整体”进行切割,将其中的“部分”用新的数表示。把1平均分成n份,其中的1份就是1/n,由此产生单位分数,把单位分数作为“分数单位”可以表达更多的分数。小数是特殊的分数,即分母是10、100、1000……的分数,同样是表达小于1的数。小数的表达同自然数一样,也是以十进制的方式用数位(计数单位)和数字表达。所以,分数和小数也是由计数单位累加产生的,只是它们的计数单位是“均分”得到的。由此可知,自然数、分数和小数都是对数量的抽象表达,虽然表达的意义不同,但是表达的方式一致,都是用“个数+计数单位”表示[4],都是对计数单位多少的表达。也就是说,计数单位这个核心概念体现了数概念本质上的一致性,能打通不同的数之间的联系。
(二)数概念的一致性源于数概念指向的核心素养一致
新课标指出,小学阶段“数的认识”的教学,要让学生“初步体会数是对数量的抽象,感悟数的概念本质上的一致性,形成数感和符号意识”[5]。数是用抽象的符号表达数量。为了简洁有效地记数,人类经历了漫长的过程。从实物符号到象形符号再到抽象符号,从许多符号到十个符号,记数符号的发展历程就是人类记数活动的发展历程。在认数过程中,学生不断感悟符号具有的数学功能,理解符号表达的现实意义,感受抽象的数可以用来解释各种各样的具体的数量,培养符号意识。同时,数的抽象过程依赖现实的背景,是现实中数量的提取。无论自然数、分数还是小数,认识的过程都是先从现实背景中抽象,再脱离现实背景建立一般性的表达,最后应用于具体问题。在这样的过程中,学生可以增强对数与数量、数量关系的直观感悟,培养数感。以自然数为例,自然数概念教学虽然分布在第一、第二两个学段,但是,都要让学生通过学具,在丰富的认数活动中,充分感悟数与数量的关系,发展估计意识,形成主动理解数和自觉运用数的能力。当然,虽然不同学段数感培养的目标一致,但是,学生认知的特点不同,因而数感培养的侧重点也略有不同。例如,第一学段“20以内数的认识”侧重于引导学生感悟数有基数和序数两层含义,“100以内数的认识”和“万以内数的认识”侧重于让学生感受位值制思想。第二学段“大数的认识”侧重于让学生感受数级和无限思想。由上可知,尽管数表达的意义不同,但是培养学生的核心素养目标一致,都要培养学生的数感和符号意识。
二、如何帮助学生感悟数概念的一致性
(一)整体分析“数的认识”内容,凸显计数单位的统领作用
根据上述对数概念一致性的认识,帮助学生感悟数概念的一致性,关键是带领学生体验计数单位在数概念建构中的统领作用,感悟不同的数都是对计数单位多少的表达(从中学生能够深度理解数概念,发展数感、符号意识和推理能力)。因此,教师需要整体分析“数的认识”内容,从而在各个单元的教学中,凸显计数单位的统领作用。
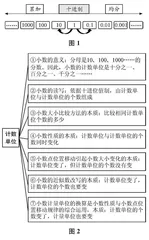
以苏教版小学数学五年级上册《小数的意义和性质》单元为例。小数与整数的计数方法都是十进制计数法,不同计数单位的累加和均分就构成了全部的整数和小数(如图1所示),因此,十进制与计数单位是本单元所涉及的核心概念。教学中,可以十进制、计数单位为核心统领本单元内容(如图2所示),从而帮助学生在深刻理解小数意义的同时感悟数概念的一致性。
实际上,基于整体分析,教学现行苏教版小学数学教材中“数的认识”相关单元时,都应该设计一些凸显计数单位统领作用的教学活动。具体如下页表1所示。
(二) 充分经历数数的过程,感受数是计数单位的累加
数(shù)源于数(shǔ)。数数是基于计数单位进行的,可以让学生充分感受到数是计数单位的累加。教学中,教师要遵循学生的认知特点,选择合适的学习素材,组织丰富的数数活动,引导学生充分经历数数的过程。
第一学段,可以从生活素材出发,重视自然数的基数和序数含义。例如, “认识11”的教学,可以先设计“数一堆无序摆放的小棒”活动,让学生理解11是11个一累加而得的;再把10个1根捆成一捆,让学生认识1个十,理解11还可以看成由1个十和1个一累加而得。
再从生活素材逐渐走向数学的结构化素材,凸显位值制思想。例如,“认识万以内的数”的教学,可以设计拨珠子的活动,让学生在计数器上先拨出2688,说出数的组成,再选一个数位拨两颗珠子,写出这个数,并说出它的组成。设计拨珠子的活动,是为了让学生用不同的计数单位数数。两颗珠子拨在个位,是计数单位“一”的累加;拨在十位,是计数单位“十”的累加……学生体会到数是由计数单位累加得到的,相同数量的珠子在不同的数位上表示的含义是不同的,进一步认识位值制和十进制。
最后可以创造无固定结构的素材,让学生以经验为媒介,通过类比推理开展隐形的数数活动。例如,给出3个苹果、4根香蕉、2个橘子、6个梨、1个草莓的图片,告诉学生“它表示300400261”,让学生再添加3个相同的水果,按规律写一写得到的数,并说一说是怎样数的。用水果代替数位顺序表,引导学生观察、推理、读数、写数,体会计数单位的变化,进一步感受数是由计数单位累加而得的。
(三)充分经历比较的过程,感受计数单位是数概念的共同本质
通过不同数知识之间的比较,能进一步帮助学生发现计数单位是数概念的共同本质。
在新授课中,可以安排沟通比较的活动,让学生充分感受数概念之间的联系。例如,在“小数的初步认识”教学的回顾环节,可以引导学生从“1”出发,不断平均分成10份,产生0.1、0.01、0.001……从而建立小数部分的计数单位体系;接着引导学生反向思考,从0.001出发,发现10个0.001是0.01,10个0.01是0.1,10个0.1是1,10个1是10……
进一步感知不管是整数部分还是小数部分,相邻两个计数单位之间的进率都是十。由此,从整数系扩充至有理数系,为后续小数的进一步研究积累认知经验。
在单元复习课或总复习课中,应该安排更为丰富的沟通比较活动,引领学生发现数概念的共同本质,实现数知识的融会贯通。例如,在六年级“数的认识”总复习中,可给出生活中的一些数,如6、1、0.5、45、-1、862,并出示
一条直线,让学生想一想:要在这条直线上找出这些数,先确定谁的位置?为什么?确定好0、1、-1的位置后,再让学生说一说:怎样在这条直线上找出6的位置呢?得出方法:数出6个这样的一格就得到6的位置。得到结论:6是6个一的累加。依次类推:862是862个一的累加,可以写成862=862×1。同时说明:“1”很关键。将“1”不断地累加(一个一个地数),满十进一,产生了新的计数单位“十”,10个一就是1个十;再将“十”不断地累加(十个十个地数),满十再进一,产生了新的计数单位“百”,10个十就是一个百……有了计数单位,862还可以用8个百、6个十和2个一来表示,写成算式862=8×100+6×10+2×1,其中100、10、1是计数单位,8、6、2是计数单位的个数。由此可知:整数就是计数单位的累加。再研究小数与分数,0.5=5×0.1,是5个0.1的累加;45=4×15,是4个15的累加。由此得出:整数、小数和分数在表达形式上有一致性,都是计数单位的累加。
参考文献:
[1] 史宁中.数学课程标准修订与核心素养[J].教育研究与评论,2022(5):2122.
[2][5] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022:85,18.
[3] 巩子坤,史宁中,张丹.义务教育数学课程标准修订的新视角:数的概念与运算的一致性[J].课程·教材·教法,2022(6):46.
[4] 史宁中,曹一鸣.义务教育数学课程标准(2022年版)解读[M].北京:北京师范大学出版社,2022:132.
*本文系江苏省2023年度教师发展研究重点课题“育人方式变革视域下的小学数学‘五育融合’研究”(编号:jsfzc15)的阶段性研究成果。