数学思维可视化“三法”

摘 要：数学知识比较抽象，为了减少数学知识的认知难度和理解难度，考虑到小学阶段学生的思维以形象思维为主，教师应通过直观、生动、具象化的手段，将学生不可见的思维活动呈现出来。在小学数学教学中，可借助直观教具、信息技术、思维导图等方式，促进学生思维可视化。

关键词：小学数学；思维可视化；教具；信息技术；思维导图

数学知识比较抽象，为了降低数学知识的认知难度和理解难度，考虑到小学阶段学生的思维以形象思维为主，教师应通过直观、生动、具象化的手段，将学生不可见的思维活动呈现出来，即思维可视化。在小学数学教学中，我们可借助直观教具、信息技术、思维导图等方式，促进学生思维可视化。

一、借助直观教具，形象地展示思维过程

教具是辅助教学的常规手段。直观教具的运用，可以帮助学生生动地理解相关的知识，形象地展示思维过程。

例如，教学苏教版小学数学一年级上册《数的分与合》一课时，多数教师会直接让学生背诵一个数可以分成几和几、几和几合成几，然后让学生反复抄写分与合的几种情况，再机械地训练加法和减法。这样的教学，不仅让学生对知识的来龙去脉少了探究的过程，而且也少了思维和构建过程的探索。而教师借助实物教具，通过直观演示——让学生动手分一分，可以让知识和思维都可视化。如“6的分与合”的教学，教师借助橘子这样的实物教具，通过分橘子给甲、乙二人的演示活动，让学生清楚地看到第一种分法是甲1个、乙5个，第二种分法是甲2个、乙4个，第三种分法为甲3个、乙3个，第四种分法为甲4个、乙2个，第五种分法为甲5个、乙1个。这样，6的5种分法，学生直观、形象地感知到了，也从中发现了规律：每多给甲1个，乙就少一个。接着，教师让学生拿出学具——6个小圆点，自己动手分一分、摆一摆，更增添了数学知识的直观性。

又如，教学《100以内的加法》一课时，教师给出算式42＋30，同步借助小木棒进行直观教学：先从小棒中拿出10根捆在一起代表10，用4捆小棒表示40，用2根小棒代表2，将4捆小棒和2根小棒放在左边；再将算式中的30用3捆小棒表示，放在右边；然后，将左边的小棒和右边的小棒放在一块，就有7捆小棒和2根小棒，得到72。于是，42＋30＝72。这样的演示过程，不仅增强了学生对算理的理解，而且提高了学生的思维力和解题能力。

二、运用信息技术，直观地演示思维过程

信息技术是促进思维可视化的重要教学手段，其中，微课、微视频、多媒体、学科软件等是典型的代表。信息技术的运用，有助于学生对新知识的理解、对重点难点的掌握，更有助于生动直观地演示思维过程。

微课、微视频的运用，可以帮助学生突破重点、理解难点。以苏教版小学数学四年级上册《确定位置》一课教学为例。这节课要求学生掌握用数对的方式表示人或物的位置；学会建立图表，根据已知的数对，在图表中找出数对所在的位置。这些知识的教学，如果采用传统的讲授法，学生会感到抽象且难以理解;而如果运用微课、微视频，就可以帮助学生直观理解。教师在录制微课时，先直观地展示数对图表的绘制方式，让绘制数对图表的思维过程可视化。学生通过观看微课，掌握绘制数对图表的方法和步骤。微课中，呈现出绘制图表的方式呈现后，教师提出一个任务：运用（4，1）、（6，4）、（4，4）等数对，建立一个图表，再在建立的图表中找到这三个点，依次连接起来，看看组成了什么样的几何图形。学生思考、交流后，教师继续用微课将这个任务的思维过程演示出来，再次帮助学生直观、生动地掌握这类一问题的解决方法。

除了微课、微视频可以促进思维可视化，运用希沃白板、小海螺软件、101教育PPT等工具，都可以将知识更形象、直观地展示给学生，在增加课堂趣味性的同时，加深学生对所学知识的理解。例如，教学苏教版小学数学一年级下册《人民币的认识》一课时，教师运用希沃白板，为学生创设日常生活中人们在超市购物的场景，通过展示人们结算、付款、找零等细节，帮助学生直观感知元、角、分的应用，让抽象的知识形象起来，也让课堂变得生动、活泼。

几何画板等数学软件，也可以促进思维可视化，帮助学生更好地理解抽象的概念和公式的推导，直观形象地掌握知识、发展能力。

例如，教学《梯形的面积》一课，教师利用几何画板提供“做数学”的机会，让学生主动发现、自主探索梯形的面积计算公式。学生通过操作经历知识的探索过程，强化知识的发生、发展和形成过程。

三、依托思维导图，清晰地画出思维过程

思维导图也叫心智图，是一种发散性的、简单且有效的思维工具。其特点是图文并茂，把各级主题的关系，用相互隶属或者相关的层次图表现出来，形成独特的思维图例，让碎片化的知识形成一个整体。在小学数学教学中，依托思维导图，可以清晰地画出思维过程。

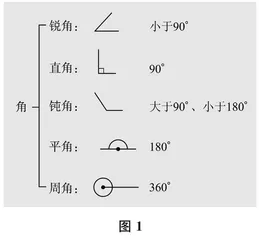
以苏教版小学数学四年级上册《角的分类》一课教学为例。对锐角、直角、钝角、平角、周角等的认识，有教师采用“一言堂”的方法进行定义式的讲解，让学生死记硬背角的分类，诸如360°的角是周角、180°的角是平角、大于90°小于180°的角是钝角等。如此教学，学生被动接受，缺少思维的活力。对此，教师可依托思维导图（如图1所示），和学生一起画出角的分类的思维过程。

形式直观、内容简洁、图文并茂的思维导图，让学生直观感知到“角”可以分为锐角、直角、钝角、平角、周角等几类；再分别给出一个角，让学生可以直观地将图形所代表的角和角的分类联系起来，实现了数形结合；然后让学生亲自量一量给出的角的大小。这样，学生就能深刻认识各种角的特点，在脑海里建立各种角的形象。这种直观的思维认知，更能帮助学生解决与角有关的数学问题。

思维导图不仅可以帮助学生构建知识体系，还有助于启发学生推理探究。以苏教版小学数学四年级下册《四则混合运算》一课教学为例。教师首先以“0”和“四则混合运算”为核心词，分别在核心词的四周呈现出“0＋任何数＝原数”“任何数－0＝原数”“任何数×0＝0”“0÷任何数＝0”“0不能作除数”等（如图2所示）。再以“运算法则”为核心词制作思维导图：

如图3所示，在“运算法则”周围，分别以“加法交换律”“加法结合律”“乘法交换律”“乘法分配律”“乘法结合律”等作为二级核心词；再分别在二级核心词旁边，运用字母表示运算法则，如在“加法交换律”上面写出“a＋b＝b＋a”。这样，学生在制作思维导图以及观察思维导图的过程中，感受数学思维的递进，同时发展抽象概括能力、类比思维能力。

总之，数学知识抽象、复杂，为了帮助学生更好地理解知识、发展能力、感悟思想、积累经验，需要在教学中尽可能地促进学生思维可视化，并探索科学的教学方式，使学生能自主发现和提出问题、分析和解决问题，主动展开思维，最终提升核心素养。