例谈“探索规律”板块内容的教学
作者: 吴建亚 顾燕
摘 要:“探索规律”这一板块的内容有其独特的学习价值——通过探索规律的活动,引领学生在实践探索中学,在问题引领下研,让学生产生对数学规律的兴趣,初步形成探索规律的意识;发展数学思维,积累探究经验,感悟数学思想。在教学中,教师应特别关注:带领学生体悟价值,激发探索兴趣;操作实践,强化探索体验;完整经历,丰富探究经验;推演说理,深化探索思维。
关键词:小学数学;探索规律;数学思维
在小学数学教学中,“探索规律”这一板块的内容有其独特的学习价值——通过探索规律的活动,引领学生在实践探索中学,在问题引领下研,让学生产生对数学规律的兴趣,初步形成探索规律的意识[1];发展数学思维,积累探究经验,感悟数学思想[2]。这一板块内容与其他板块内容相比,具有知识呈现隐蔽、探索过程复杂、学习能力综合、思维要求高等特点,需要教师在教学中特别关注激发探索兴趣、强化探索体验、丰富探索经验、深化探索思维四个关键点。
一、体悟价值,激发探索兴趣
波利亚指出:“为了有效地学习,学生应当对所学习的材料感兴趣并在学习活动中找到乐趣,这是最佳的动机。”[3]“探索规律”的教学也需要提供学生感兴趣的学习材料,让学生感受知识的奇妙,体悟数学规律的价值。教师可以借助情境,挖掘出数学规律深层次的价值,巧妙地向学生展现数学魅力,激发学生对获得规律的诉求。
例如,苏教版小学数学五年级下册《和与积的奇偶性》一课,教师创设了“神机妙算”的情境,开展了如下教学过程:
师 同学们,今天我们来玩一个跟学号有关的小游戏。请第二组学号是奇数的同学起立!
(5位学生站起来。)
师 见证奇迹的时刻就要来了!这一组有5位同学站着,把他们的学号表示的数相加,和是奇数。你们相信吗?
(学生议论纷纷。)
师 让我们来验证一下。
(起立的学生依次报学号,其他学生计算。)
生 和是113。
师 说对了!再来一次怎么样?这回你们选一个组。
生 第四组。
师 那就请第四组学号是奇数的同学站起来。
(4位学生站起来。)
师 这次要增加点难度了。请这4位同学全部坐下,把这一组所有同学的学号表示的数相加,和是偶数。
(全班计算验证后纷纷发出惊叹声。)
师 老师都不用知道同学们的学号,就能判断出了和是奇数还是偶数,厉害吧?其实呀,我只是比你们早知道了藏在里面的秘密罢了,想不想和老师一起来探索其中的规律?
兴趣是动力之源。一个“神机妙算”的情境,让学生在惊叹中感受到了和的奇偶性规律的价值,他们想探索这个规律的动力被快速唤醒。有了自我内在的需求,学生被激发的兴趣持久性更强,而浓厚的兴趣会使他们在整个探索过程中都保持强劲的学习动力。
二、操作实践,强化探索体验
如何在激发学生兴趣后,引领学生主动参与探索活动?沈重予老师说:“现实情境里的现象、问题或操作活动,是引发学生进行探索的‘诱因’,要积极运用这些‘诱因’引导并鼓励学生开展探索活动。”巧妙的操作活动,有利于强化学生的探索体验,增强学生的探索意识。
例如,苏教版小学数学六年级上册《表面涂色的正方体》一课,教师组织学生开展了“切正方体泥块”的操作活动。
师 瞧,老师带来了一个泥块,它有什么特点?
生 它是一个正方体,有8个顶点,12条棱,6个面,每个面完全相同。
师 老师把这个正方体泥块表面涂上了红色。如果我把每条棱都平均分成2份。照这个样子(切面与棱垂直)把它切开,会发生什么情况呢?
(教师拿出泥块,演示切开的过程。)
师 观察一下,老师切出了多少个小正方体?都有什么共同点?
生 切成了8个一样大的小正方体,每个小正方体都有3个面是红色的。
师 你想来切一切吗?
生 想!
师 想一想你准备把棱平均分成几份?怎样切,能保证切出的每一份都是正方体?想好了,就可以开始切了。
(学生小组拿出表面涂上红色的正方体泥块,开展“切一切”的活动。有的小组把棱平均分成3份来切,有的小组把棱平均分成4份来切。)
师 我发现你们把每条棱平均分的份数都比我多,切开后的情况跟我的一样吗?
生 有的小正方体是3个面涂色,有的是2个面,有的是1个面,还有的小正方体6个面都没有涂色!
师 同样是把大正方体切成小正方体,我只切出了一种情况——都是3面涂色的小正方体,你们怎么可以切出这么多情况呢?把每条棱平均分成3份的同学和平均分成4份的同学,小正方体的涂色情况相同吗?请以小组为单位探究这两个问题。
……
师 如果把每条棱平均分成5份,切出来的小正方体中,3面涂色、2面涂色和1面涂色的分别有几个?如果把每条棱平均分成7份呢?不操作能得到答案吗?
……
师 这节课我们一起探索并找到了表面涂色的正方体中隐含的规律,你们都很棒!不过,老师又有一个新问题:如果要得到96个2面涂色的小正方体,该把大正方体的每条棱平均分成几份呢?请大家课后去研究,下节课把答案告诉我。
切泥块的操作活动,符合学生喜欢动手操作的年龄特点,能够吸引学生热情参与。而每一次活动前的设问、活动后的追问,可以及时引领学生对操作目标和操作结果进行积极思考。精心设计的操作活动和一系列问题,步步引人入胜,推动学生饶有兴趣地展开探索活动。学生经历动手操作、观察对比,以及对现象进行思考和分析,在操作实践中获得成功的快乐,强化探索体验。
三、完整经历,丰富探究经验
探索规律的过程比获得规律更重要。在探索规律的过程中,思考确定探索规律的方向,是关键环节。然而,很多教师却往往忽略它,直接告知方向并带着学生按照指定的方向去探索,导致学生经历的探索过程是不完整的,积累的探索经验也是残缺的,甚至是贫乏的。因此,教师应重视引导学生经历完整探究过程,丰富探究经验。
例如,苏教版小学数学五年级上册《钉子板上的多边形》一课,有如下教学过程:
师 大家都感觉到了,钉子板上多边形的面积有大有小。你有没有想过,钉子板上多边形的面积可能会与什么有关呢?
生 与边上的钉子数有关,我感觉边上的钉子数越多面积越大。
师 如果边上的钉子数一样,那么面积一定相等吗?比如,几个多边形的边上都是4枚钉子,它们的面积相等吗?
(学生思考。)
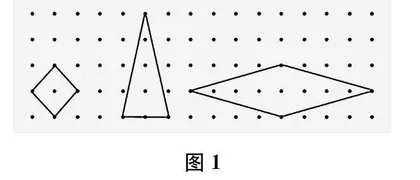
师 (出示图1)
老师这里有一组图,它们的面积相等吗?
生 不相等。
生 与内部的钉子数有关,我感觉内部的钉子数越多面积越大。
师 那么,是不是内部的钉子数一样,面积一定相等呢?(出示图2)
老师再给你们一组图。
师 通过刚才的两次观察思考,我们知道,边上的钉子数相等,面积不一定相等,内部的钉子数相等,面积也不一定相等。所以——
生 钉子板上多边形的面积与边上的钉子数和内部的钉子数都有关。
钉子板上多边形的面积到底与什么有关?在思维没有方向的时候,创设“猜一猜”的情境,引导学生提出两个猜想——“边上的钉子数越多,面积越大”“内部的钉子数越多,面积越大”。面对学生两个不全面的猜想,教师顺着他们的思维,相机出示两组图,引发认知冲突,促使他们对自己的第一感觉进行反思。学生逐步补充、完善自己的想法,慢慢地意识到钉子板上多边形的面积可能既与多边形边上的钉子数有关,又与多边形内部的钉子数有关,从而为接下来的探索规律聚焦方向。这样的设计,不仅帮助学生学会思考,还指导学生学会探索,丰富并积累了寻找方向的探索经验。
四、推演说理,深化探索思维
理解是建构的关键环节。在探索规律的过程中,教师可以设计推演说理的学习活动,促进学生对规律本质的理解,深化规律探索的数学思维。
例如,“和与积的奇偶性”与前几册中以现实生活为背景的“探索规律”活动比,研究的是更为抽象的数学现象,这对学生而言是个新的挑战。不仅如此,多个自然数相加和的奇偶性以及相乘的积的奇偶性规律本身比较隐蔽,学生很难从几个简单的例子中找到其中蕴含的规律。因此,在学生隐约发现了规律后,教师创设合适的情境,组织学生推演说理,促进学生深度理解规律本质。
师 刚才,大家通过举例,发现不管几个数相加,加数中如果有1、3、5……个奇数,和就是奇数;如果有2、4、6……个奇数,和就是偶数。为什么有这样的规律呢?谁能来跟大家讲讲其中的道理呢?
(学生沉默。)
师 看来同学们一时也想不明白其中的道理,没关系,我们先来做个“连连看”小游戏。规则是:在算式中,每遇到两个奇数,就把它们连在一起,看你们有何发现。
(学生在自己刚才举例的算式上操作。)
生 我们发现,所有的算式只有两种情况:一种是多出一个奇数;另一种是正好都连完,没有多余。
生 多出一个奇数的算式,和是奇数;正好都连完的算式,和是偶数。
生 (展示如图3所示的算式)
奇数+奇数,和是偶数,连在一起的2个奇数就可以看成1个偶数。2个奇数连在一起就像配对,如果加数中的奇数都能配成对,说明有偶数个奇数,和一定是偶数;如果最后还剩一个奇数,说明有奇数个奇数,和一定是奇数。
……
带领学生举例、观察、比较、分析、提出猜想、再举例验证后,很多教师会进入运用规律解决问题环节。其实,没有经历说理的辨析过程,学生对这个规律的理解还是不透彻的。“连连看”游戏,唤醒了学生已有的认知经验,引导学生运用对应思想把两个奇数加以配对看作一个偶数。有了这个解释规律的思维操作环节,学生很容易理解和的奇偶性规律,深化了探索规律的数学思维。
参考文献:
[1] 沈重予.直面现象把握本质——谈“探索规律”的教材和教学[J].教育研究与评论(小学教育教学),2011(8):10.
[2] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012:44.
[3] 徐利治,王光明.数学方法论选读[M].北京:北京师范大学出版社,2010:54.