多想想“学生会怎样思考”

摘要：数学知识是客观的，而学生的认识是主观的，学生对于数学知识的建构是依赖于个人经验的。实际教学中，教师往往会从自身对知识的理解出发组织教学活动，意识不到同样的问题在学生的眼中是复杂且有挑战性的。教师要多想想“学生会怎样思考”，在学生经验与学科知识之间搭建利于学生建构新知的通道。通过对《认识11—20各数》一课教学案例的分析与改进，说明如何基于学生的已有经验设计并实施教学。

关键词：学生经验;教学诊断;《认识11—20各数》

数学知识是客观的，而学生的认识是主观的，学生对于数学知识的建构是依赖于个人经验的。正如大家熟悉的一个例子中所描述的那样：“鱼在水中生活，不了解陆地上发生的事情，因此向青蛙打听。青蛙向鱼描述了陆地上的鸟、牛、人等。鱼根据青蛙的描述，在头脑中想象出丰富的画面：鸟是在鱼身上长着翅膀的，牛是在鱼身上长有四条腿的，人是在鱼身上长着四肢用鱼尾走路的。鱼根据自身的经验对新知识进行了重构。”数学学习过程也是学生借助外部环境对学习素材的加工、重构。教师必须了解学生的认知建构过程，并且从学生的建构视角出发去设计教学环节，帮助他们在自身经验的基础上更合理地认识所学习的数学知识。

然而，教学中，教师往往会从自身对知识的理解出发组织教学活动，也就造成了很多教师（尤其是新教师）会面临的教学困惑：“这个例题太简单了，最多20分钟就全都教完了，怎么才能上满40分钟呢？”教师意识不到同样的问题在学生的眼中是复杂且有挑战性的。对此，多想想“学生会怎样思考”，在学生经验与学科知识之间搭建利于学生建构新知的通道，教学便会顺畅高效很多。下面，通过对一个教学案例的分析与改进来说明。

一、案例描述

W老师是新教师，教态亲切，能和所教的一年级学生很好地交流沟通，教学工作认真负责，经常阅读教育杂志中的教学设计，并且会在备课和课堂教学中借鉴使用。她执教苏教版小学数学一年级上册《认识11—20各数》的片段如下：

师（课件出示一些贴纸）同学们，这儿有多少张贴纸呢？我们一起来数一数。

（全班学生一起数，数出有12张贴纸。）

师你能用小棒表示吗？请你数出12根小棒，贴在小磁板上，同桌互相检查数得对不对。

（学生数小棒，同桌互相检查。多数学生是将12根小棒堆在一起数的，也有学生将12根小棒1根1根地摆成一排。）

师你能动手移一移，摆一摆，让人一眼就看出是12根小棒吗？

（学生调整小棒的摆放，等学生摆好后，教师选择学生的小磁板贴在黑板上展示。）

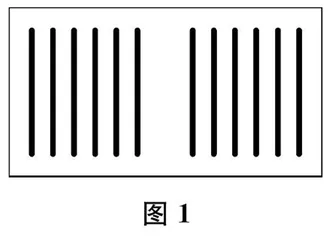
师（板贴第一种摆法，如图1所示）他是怎么摆的？是12根吗？我们一起数一数。

生是12根，左边有6根，右边有6根。

师6根6根地摆，是12根吗？（生答“是”）能一眼看出来吗？（生答“不能”）不能一眼看出来，要数才知道。（板贴第二种摆法，如图2所示）他是怎么摆的？

生他是3根3根摆的，3、6、9、12根。

师能一眼看出来是12根吗？

生能看出来。

师（板贴第三种摆法，如图3所示）这位同学是怎么摆的？

生他是2根2根摆的。

师能一眼看出是12根吗？

生能。

师能吗？

生能。

师（板贴第四种摆法，如图4所示）看这位同学的摆法。

师左边摆了10根，右边摆了2根，能一眼看出是12根吗？

生能。

师我们通常是这样做的，数出10根小棒，就捆成1捆。10根1捆，就是以前学过的10个一是1个十，谁能这样说一说。

（教师出示图5，并请学生复述。）

师反过来，就是1个十是——（生答“10个一”）现在好摆了吧。像这样调整一下，把10根小棒捆成1捆，再摆一摆，摆出12来。

（学生按教师的要求，将10根小棒捆成1捆，再摆2根小棒。）

师现在我们怎样摆12根小棒？

生先摆1捆，再摆2根。

师古人也是这样摆的。

（教师介绍数学史，讲述石子计数的方法，再将石子替换成小棒。）

二、案例分析

上述片段仅仅是新授课的一部分，后续的教学过程有序、开放，练习层次分明，W老师上了一节很好的数学课。就这一教学片段而言，我们对一个现象非常感兴趣：当W老师提问“能一眼看出是12根吗”，学生对不同的摆法基本都说“能”。这是为什么呢？

先来看教学内容。在学习本节课之前，学生已经认识了10以内的数，能正确、熟练地计算10以内的加、减法。绝大多数学生都已经接触过比10大的数，因此，本节课的教学难度似乎不大。而本节课的教学内容又非常重要，因为对11—20各数的认识是20以内进位加法和退位减法的基础。要使学生掌握11—20各数的读写，必须先让学生理解这一个数里有几个十和几个一。因此，教材首先从学生的已有经验出发，组织学生通过操作活动先认识“10个一是1个十”，以此为基础继续摆小棒，使学生在具体的操作活动中认识11—20各数。配套教师用书中明确指出，本节课要组织三个层次的认数活动：第一层次，认识“10个一是1个十”;第二层次，认识12;第三层次，认、读11—20各数。

不难发现，W老师基本省略了第一层次，直接开始从认识12入手。W老师认为，如果从第一层次入手，似乎给了学生较多的暗示，学生虽然更容易摆出1捆加2根小棒来表示12，但是这样的教学局限了学生的思维，没有尊重学生的学习主体地位，而且开放性不够。所以，W老师借鉴了他人的教学设计，请学生自己摆出12根，这样学生就会有不同的摆法;再通过“怎样让人一眼看出来是12根”这样的提问，让学生比较不同的摆法，发现用1捆加上2根小棒最方便。W老师对于课堂中的生成（问学生“能一眼看出是12根吗”，学生基本都回答“能”）也很困惑。按照她的预设，对于其他的摆法，学生应该都会回答“不能”，然后通过比较优化摆法，从而体会用1捆小棒表示10根来摆小棒最方便。

学生为什么对不同的摆法基本都说“能”呢？课后，笔者和学生进行了交流，发现学生说“能”的原因有这样几方面：这些摆法是学生自己摆出来的，而且他们知道这些小棒是12根;对教师的提问“能一眼看出是12根吗”，学生也有不同的理解方式，他们会将问题理解为“你知道这里有12根吗”;另外，低年级学生总是期待自己的学习行为得到老师的肯定，因此要表现出自己“能”的样子。

怎样真正帮助学生理解用1捆小棒和2根小棒合起来表示12最好？其本质在于规定了1捆小棒就表示1个十，因此在数小棒的根数时，看到1捆就知道表示1个十，只需要再数单根的小棒有多少根，和1个十合起来就是十几。让学生认识这点需要有相应的体验活动。学生的不同摆法都是对“12”的不同表示方式，因此在关注摆法优化的同时，也可以关注多样化，因为这样可以丰富学生对12这个数的认识——12可以是12个1，也可以是2个6，还可以是1个十和2个一，等等。

和W老师反馈了学生的想法，她说：“真没有想到学生会这样想。”是啊，教学设计需要尊重学生的现实经验，了解学生的思维活动，这是非常重要的。对教师来说，面对学生的不同回答，不应该用“正确”或“错误”这样简单的判断为指向，而是更应该关注学生为什么会得到这样的结果，通过让学生复述自己的思考过程，再现思维活动，从而了解学生的真实想法。我们所说的尊重学生，需要蹲下来和学生说话，但这只是一种外部行为，而了解学生、从学生的现实经验出发设计教学过程才是尊重学生的核心。

三、案例改进

上述《认识11—20各数》一课教学，可做如下的改进：

（一）情境引入

师小熊在文具店买了一些铅笔，你能数一数小熊一共买了几支铅笔吗？

（课件呈现情境图，学生数出一共有12支铅笔。）

师刚才啊，我们是一支一支地数，数出有12支铅笔。如果请你用小棒表示铅笔，你能想一个好方法让人一眼就看出有12支吗？想一想，在小磁板上展示你的摆法。

（学生在小磁板上摆小棒，教师巡视，并选择不同的摆法贴在黑板上。板贴如图6所示。）

（二）比较优化

师同学们真厉害，想到了这么多不同的摆法。下面请这五位同学自己说一说，你是怎么摆的。

生我是2根2根摆的。

师我们一起数一数，2，4，6，8，10，12。同学们，摆几个2就是12？

生摆6个2就是12。

生我是3根3根摆的。

师你带着同学一起数一数。

（全班学生齐数：3，6，9，12。）

师3根3根地摆，摆几个3就是12？

生摆4个3就是12。

生我是先摆2个5根，就是10根，再摆2根就是12根。

生我先摆6根，再摆6根，就是12根。

生我先摆10根，再摆2根，就是12根。

师谢谢同学们的发言。真没有想到，12有这么多不同的摆法。可以是6个（生答“2”），还可以是4个（生答“3”），还可以是2个5，再添2根，还可以是2个6，还可以先摆10根，再摆2根。自己摆，只能想到一种摆法;互相说一说，我们就知道了更多的摆法。（稍停）看最后一种摆法，前面我们学过10根可以捆成1捆。

师（出示图7，将最后一种摆法中的10根用皮筋捆成1捆）这捆小棒有几根？

生10根。

师把10个1根捆成1捆是10根，就表示1个十。我们就说10个一是1个十，反过来，1个十里有——

生10个一。

师我们看到1捆，就知道它表示1个——

生十。

师这五种摆法，你认为哪一种能让人一眼就看出来是12根？

生最后一种摆法一眼就能看出来，因为看到1捆就是10根，再加上2根就是12根了。

生我喜欢第四种方法，因为2个6很容易看出来。

师同学们的想法还不同呢。下面，老师要用这些方法再摆一个数，（出示图8）你能一眼就看出老师摆的是多少吗？

生摆的数是14。

师这四幅图中的小棒都表示14，你们是看哪幅图知道这个数是14的呢？

生我看最后一幅图，一眼就看出来了，1捆是10根，还有4根，就是14。

师是啊，前面的图虽然也表示14，但是都需要数才知道。我们一起数一数。

（教师带领学生数出前三幅图中的小棒数。）

师但是第四幅图，我们一看到1捆，马上就知道它表示一个十，只要看后面有4根，就能知道是14了。这个办法好不好？请同学们也数出10根小棒捆成一捆。

（学生数出10根小棒捆成1捆。）

师你能用这样的方法摆出11根小棒吗？

……

改进后的教学，尊重了学生的原有经验。在展示了12的多样化摆法之后，首先帮助学生丰富对12的认识。学生对同一个数的表示方法越多，对这个数本身的认识也就越丰富，这也是在认数活动中发展学生数感的方法。我们期望学生看到“12”时，不仅知道它是由1个十和2个一组成的，还知道其他的表示方法（如2个6、3个4等）。然后在学生体验的基础上优化摆法。先建立“10个一是1个十”的概念，并且明确“看到1捆就知道表示1个十”——正是因为知道1捆表示1个十，在看到1捆时就可以省略数的过程，这才是这种摆法最好的原因。在此基础上，呈现14的不同摆法，学生就很容易发现这种摆法的优势，并自然达成对摆法的优化。