为“真学”而教

摘要：“两、三位数除以一位数的笔算”这部分内容的教学，存在不少“假学”的情况。由此，提出为“真学”而教的应对举措：让学生“真学”，就要站在学生的立场上思考问题，找准学生理解的障碍点，帮助学生突破认知定式;要紧紧抓住知识的本质开展教学，引领学生经历完整的操作过程;要正视学生的学情，让学生在深刻理解的基础上，真正接受知识。

关键词：“真学”;“假学”;认知定式;过程;理解

近几年，许多教育界的学者发出了“让学习在课堂上真正发生”的呼吁。笔者也不禁反思：在当下的数学课堂上，学生的学习是否真正发生了？是否存在“假学”现象？如何为“真学”而教？在一些教研活动中，笔者听过不少教师教学“两、三位数除以一位数的笔算”这部分内容，发现存在不少“假学”的情况。由此，提出为“真学”而教的应对举措。

一、要突破认知定式

（一）案例描述

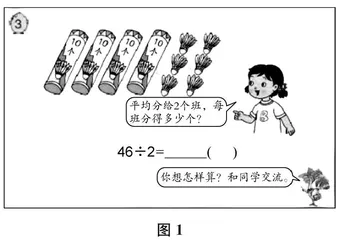
师（出示图1）瞧，一位小朋友去买羽毛球，你从图中收集到了哪些信息，又提出了怎样的问题？

生一共有46个羽毛球，平均分给2个班，问每个班分得几个羽毛球。

师那你会列式吗？说说你是怎样算的？

生46÷2=23（个），我是像乘法计算那样，先算个位6÷2=3，再算十位40÷2=20，最后算20+3=23。

师我们也可以先算十位40÷2=20，再算个位6÷2=3，最后算20+3=23。

（学生满脸疑惑：刚学过的乘法不是一再要求从个位算起吗？但还是纷纷点头表示赞同。）

（二）案例分析

类似上述案例，直接扭转学生的思维从“先算个位”到“先算十位”的做法非常常见。原因可能有以下几个方面：（1）苏教版小学数学教材把首位不够除（54÷2）的情况安排在了下一课时，这里不好对比沟通;（2）教师认为46÷2=23的除法竖式书写才是重点，想更快地进入除法竖式算法的教学，觉得在此纠结会浪费时间。

仔细想来：加、减、乘法竖式计算都是先算个位，怎么除法就从高位算起了？上一次学习除法还是表内除法的竖式，商就是一位数，没有关注先算哪一位，况且46÷2，先算哪一位，结果都是23，为什么教师就360度大转弯“强迫”学生先算十位了？这没有给学生的思维留出缓冲的时间和空间，没有对先算个位的想法作出相应的肯定。这样的教学有悖于学生立场，没有关注到学生的认知起点和理解障碍点，引发的是一种“假学”。

笔者以为，应该从学生已知的除法估算入手，先引导学生初步建立除法口算与乘法不同的印象，给思维一个缓冲，再引入新授内容更为妥当。

（三）案例改进

师同学们，我们来玩一个猜一猜的游戏，好不好？[板书：6（ ）÷2=？]商是几十多？你是怎么想的？

生商是三十多，因为60÷2=30。

师[板书：（ ）4÷2=？]商又是几十多？

生好像猜不出来。

师为什么不行？

生因为不知道十位是几。

师那把4换到十位呢？为什么现在又行了？

生4（ ）÷2的商肯定是二十多，因为40÷2=20。

师那你觉得做这样的除法估算的秘诀是什么？

生先算十位，用十位上的数除以除数，商就是几十多。

师看来呀，要想快速地估算出除法算式的商是几十多，还是得先算十位。那到底是四十几呢？（出示图1）我们来看这道题……

让学生“真学”，就要站在学生的立场上思考问题，找准学生理解的障碍点。障碍点在哪里，突破口往往就在哪里。针对学生“为什么先算十位”的疑惑，教师设计了估算环节，通过制造认知冲突，一下子抓住了学生的兴趣点，将思考聚焦到“除法估算先算十位”这样的核心上来，扫清了学生学习的障碍，为接下来教学“先算十位”提供了缓冲，帮助学生在大脑中初步建立乘、除法估算方法不同的印象。在此基础上，再引导学生进入例题的学习，有效帮助学生避免了旧知对新知的干扰。

二、要经历完整过程

（一）案例描述

师请大家来看，老师这有46根小棒，谁能上来摆一摆、说一说先算什么再算什么？

生先分4个十，每份2个十，再分6个一，每份3个一，合起来就是23。

师（结合图2）他说得多好呀！瞧，和我们口算的过程是一致的，都是先分4个十，再分6个一。那46÷2的口算我们掌握了，笔算该怎么写呢？

（二）案例分析

这个案例中，教师示范到位，学生将摆小棒和口算的过程融为一体，教学流程看似顺理成章、十分流畅。可是仔细想来，这里的操作只有摆小棒，而且只是一个学生上黑板分。如果换一种学具，学生还会分吗？如果只给静态的图片，甚至只给算式呢？学生头脑中已经形成口算的算法了吗？显然没有。这样的教学流程其实是不扎实的，并没有抓住算理的本质。

操作活动讲究三个层次：（1）行为操作。学生通过操作学具，如摆小棒、圆片等，得到计算结果。（2）表象操作。学生在头脑中将行为操作的过程像“放电影”一样进行回放，这是一个“压缩”的过程，作用是提炼方法，逐步从具体走向抽象。（3）符号操作。借鉴行为操作和表象操作对抽象的算式进行演算。显然，本案例中没有将行为操作落实（仅有一个学生、一种学具），忽略了表象操作和符号操作（直接过渡到了竖式书写），只能是一种流水线式的“假学”。

（三）案例改进

1.自主探究，初步理解算理

师46÷2得多少呢？你怎么算得这么快？

生40÷2=20，6÷2=3，20+3=23。

师你是根据数的组成，口算来完成的。谁能结合我们口算的过程，来摆一摆、分一分？

（学生自由操作小棒以及可以卡扣在一起的小方块、小圆片等学具。）

师大家用不同的方法算出的结果都是23。比较这些不同的方法，在计算的顺序上有什么相同的地方？结合图和算式，想一想。

生不论口算，还是分小棒、小方块、小圆片，都是先分4个十，再分6个一。

师是的，虽然方法不同，但道理都是相通的。这就是我们今天要学习的除法，简单吗？有信心了，那我们继续往下学。

2.层层递进，深刻理解算理

师（出示36根小棒的图片）3个小朋友有36根小棒，平均每人多少根？

（学生回答后，教师PPT呈现分小棒的动态过程。）

师（出示48根小棒的图片）48÷4先分什么，再分什么？

（学生回答。）

师（出示图3）246÷2这道算式有点不一样，你能看懂图吗？谁来说一说先分什么，再分什么，最后分什么？

（学生回答。）

师不知不觉中，三位数除以一位数我们都会算了，真了不起！接下来，老师继续增加难度：不给图了，你能自己在头脑中想一想吗？（出示算式：26÷2，482÷2）任选一题，说给同桌听一听。

（学生回答。）

师看来，没有图，我们在头脑中想一想同样能够算出正确答案。回忆一下，一开始我们用学具分一分，接着看图想一想，后来图也没有了，看算式直接在头脑中想一想。两位数除以一位数，都是先算什么，再算什么？分几步来算？三位数除以一位数呢？同桌两人互相交流。

（学生交流明确：两位数除以一位数，先算十位，再算个位，分两步来算;三位数除以一位数，先算百位，再算十位，最后算个位，分三步来算。）

这里，紧紧地抓住了操作活动的三个层次：第一环节，通过摆小棒、小方块、小圆片等活动完成了行为操作;第二环节，细分了“分一分，算一算”和“看一看，算一算”两个层次，实现了表象操作的目标，最后的“想一想，算一算”和小结达成了符号操作的目标。在环环相扣的同时，做到了近期和远期目标相结合，为后面进一步学习除法竖式的书写奠定了良好的基础。

三、要达成深刻理解

（一）案例描述

师我们已经能口算出答案了，但光会口算还远远不够，你会用竖式计算吗？请大家在练习纸上试一试。

（学生写竖式计算过程，错误的和正确的写法都有。）

师看来关于竖式的写法，我们发生了一些分歧。那46÷2的竖式到底该怎么写呢？我们一起来看看。（出示正确的竖式）和部分同学的写法是一致的。这个竖式这样写是有它的道理的。实际上，我们写的竖式的计算过程和刚才分小棒、口算的过程是一样的……会写了吗？那我们再来练习两道题。

（二）案例分析

这个案例中，错误写法的学生没有得到教师的关注，被忽略了。这些学生就一路看着教师的脸色，揣摩教师的心思，被迫无奈地直接接受了除法竖式的书写格式，并未真正理解为什么有这样的数学规定。如何让学生对这种数学规定在理解的基础上接受，是教师需要深入思考的问题。

（三）案例改进

师我们已经能口算出答案了，但光会口算还远远不够，你会用竖式计算吗？请大家在练习纸上试一试。

（学生写竖式计算过程，错误的和正确的写法都有。）

师（出示图4和图5）看来关于竖式的写法，我们发生了一些分歧。这是很正常的事情。下面我们请两方代表各自说一说自己的理由。

生我觉得右边的写法是对的，它更能帮助我们一目了然地看出分的过程，先分4个十，再分6个一，一步一步，条理非常清晰。

生我不同意，我们在写乘法竖式的时候，一开始也是一步一步分层写的，但是后来书上要求我们合并起来，因为这样更简洁。我觉得除法也应该这样简洁地写，所以左边正确。

生我也觉得左边正确，因为我们以前写13÷2这样的除法竖式时也是只写一层的，没有像右边那样写两层。

生我来回答你的疑问。写13÷2的除法竖式时，因为它只分了一次，所以只写一层;而这里的46÷2分了两次，所以要分两层，并不矛盾。

生我也不同意左边的写法。因为很多同学是知道口算的答案直接上商写的23，然后算2×23=46，一次性写的46，我觉得这是“假算”。以后遇到更复杂的算式，我们是不可能一次性上商的，还是应该像右边这样一步一步有条理地分层去算。

师（出示5678÷9，6789÷37）你说的是像这样的算式吗？

（学生尝试竖式上商，发现困难重重。）

师这样的除法，你也能一眼就看出结果是多少吗？

生不能。

师是的，不能一眼看出商是多少，也就不能一步分完。现在你对于这两种除法竖式有什么想说的？

生我们写除法竖式时还是应该像右边这样，先算十位，再算个位，一步一步有条理地算下去。

师老师要为刚刚发言的所有同学点赞，你们敢于质疑，敢于思考，敢于联系前面的知识，讲道理、不争吵，数学能力和品格都相当高。像右边这样写其实是有它的道理的。实际上，我们写的竖式的计算过程和刚才分小棒、口算的过程是一样的。我们来看……

上述教学中，教师“放大”了学生的分歧，把学生的疑惑拿出来“晒一晒”，放手让学生去争辩，使学生在争辩中发现错误写法的弊端，以及乘、除法在竖式书写中的异同——乘法是为了简洁，而除法不可以为了简洁而降低计算的正确率。在争辩中，除法竖式的书写格式印入学生心中，学生也获得了“带得走”的学习能力。学生只有在内心深刻理解的基础上，才能够真正接受这样的数学规定，才是“真学”。