从“特例”到“普例”

【编者按】

推理意识是《义务教育数学课程标准（2022年版）》中小学阶段核心素养的主要表现之一。推理意识作为数学学习的重要思维模式，对提高小学生的数学逻辑思维能力具有不可替代的重要作用，学生能否形成良好的推理能力，不仅仅会对数学这门学科的学习造成直接影响，同时也在一定程度上关系到学生未来的发展。云南省“兴滇英才支持计划”周佳泉小学数学名师工作室、昆明市第二批“春城计划”周佳泉小学数学名师工作室、盘龙区第四届周佳泉小学数学名师工作室历时两年，对小学生“推理意识培养”专题进行了深入探讨和积极的课堂教学实践。现将周老师团队的一些研究成果分享出来，供广大一线教师参考。

“数与形”是人教版六年级上册数学广角中的内容，形式新颖、趣味性强、思维难度大。既是代数知识与几何知识相互融合的有效途径，更是培养学生推理意识难得的载体。教材上面的例题只有两个，配套的练习却五花八门。教材似乎已经在暗示我们，本节课的教学，要让学生理解掌握普遍的通式、通法，而非专门探寻一种问题形态的特例、特式。

结合本工作室多位老师的执教体会，试析如下：

一、“数”与“形”的学习难深入

数形结合思想的核心就是将二者结合起来，用“形”的直观演绎“数”，用“数”的精准把握“形”，促进学生对于知识的理解和问题的有效解决。怎样将数与形有机结合给学生讲清楚，对于师生来说确实是一个艰巨的挑战。

1. “数”与“形”相分离。在教学中，有的问题借助图形能讲得更清楚，但不同的题方法都不同，都要带领学生从头去分析，于是有教师索性偷个懒，直接带着学生找数字规律，数出每个图的个数，变“形”为“数”，从数字的角度来发现规律；要么直接将图形依次画出来，找到规律或结果。这样的教学将“数”和“形”分离开，学生并不理解结果背后蕴藏的数学道理，对图形的特点和规律的挖掘欠缺，丢失了数形结合的意义。

“数”与“形”相分离，就让这节课明珠蒙尘，索然无味了。

2. 把“现象”当“规律”。有的老师在教学例题1的时候，从几个有限的奇数列中观察得出“规律”——“有几个连续奇数相加就是几的平方”，就把这个所谓的“规律”当成了本节课的研究结论。匆匆运用这样的结论去海量解题，让学生的思维停留在了肤浅的“现象”层面。当学生遇上类似“1+3+5+7+……+393+395+397+399=（ ）2”这样复杂的奇数列求和的问题时，学生无从知晓一共有多少个奇数，顿时束手无策。甚至在面对“1+3+5+7+9+11=62”这样简单的奇数列求和问题，也只能从所谓“规律”的角度去解释“因为有6个连续奇数相加，所以等于6的平方”，却没有办法解释背后的本质“为什么几个奇数相加就会是几的平方”。

把“现象”当“规律”，就让这节课失去了应有的深度，留于浅尝辄止的肤浅。

3. “例”与“题”难贯通。从教材的编排来看，例题与练习确实“不配套”。它不再像以往的单元那样，例题长什么样，后面的习题基本跟它长得“八九分像”。这个单元是个例外，每一题都藏着不同的规律，每道练习都像是在新授课，要一题一题地去发现规律，面对题型复杂、变化较多的练习，学生难以实现举一反三，倍感困难，难以对数与形进行更深入的探究。

二、“特例”到“普例”的进阶难贯通

要突破“数与形”的教学瓶颈，贯通从“特例”到“普例”的学习进阶是一条有效途径。学生循着这个学习进阶步步登高，“数形结合思想”的渗透和“推理意识”的发展才有章可循。然而，从“特例”到“普例”的学习进阶的构建也是充满了挑战：

1. “平方数”只是“特例”。从“1+3+5+7+……”的探究中，得出的“从1开始，有几个连续奇数相加就是几的平方”，我们称其为“平方数”。在奇数列的世界中，这条规律无往而不胜。但是到了偶数列、自然数列和其他普通等差数列时，这个规律却不灵了。

究其原因，就是奇数列只是众多等差数列中的一个特例，它不具有普遍性。

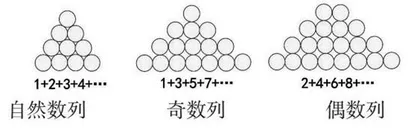
2. “梯形数”才是“普例”。通过数形结合的策略，学生不难发现：其实奇数列、偶数列、自然数列和其他普通等差数列都是“梯形数列”。（如下图）

自然数列    奇数列     偶数列

都可以用梯形面积计算公式来求和。即：（首项＋末项）×项数÷2。这样的思路让学生眼前一亮——原来梯形的面积计算公式还能这么用！

“特例”只是一枝独秀，“普例”才是天下皆春。

3. 从“特例”到“普例”的阻碍。从“特例”到“普例”的学习进阶中，最困难的地方就在于“特例”的首因效应。它会让学生误以为所有的等差数列之和都应该是一个平方数，在狭窄的视域中虽“苦苦追寻”却仍“一无所获”。打破这一阻碍的有效手段就是画图——一旦画图，学生就会豁然开朗。“数”与“形”结合起来的必要性昭之若揭。（如下图）

由此，再一次证明“数”与“形”不能分离，结合起来才能相得益彰。

三、“形”与“数”的融通探索

“数”与“形”相融通，只要运用恰当，难题往往迎刃而解。

1. “形”的直观让“数”的理解更容易。还是那个老问题“为什么几个连续奇数（从1开始）的和就会是几的平方？”“你如何判断一个比较长的连续奇数列（1开始）中奇数有多少个？”一旦把“数”与“形”相结合起来思考，问题瞬间变得很简单：

正方形的最外一层“拐弯”数就对应着奇数列中的最后一个数。把最外一层“拐弯”数“添1”再“均分”，就非常容易知道这是一个几行几列的正方形，也就是这个奇数列的和是几的平方。回到算式中，把最后一个奇数“加1再均分”，就能想出它的和是几的平方。

把“数”当做“形”，也能很容易地想出一个奇数列中有多少个数：

当我们把数列“补全”之后，原来的最后一个奇数是n，整个数列就一共有“n+1”个数，其中奇数的个数占一半，就是“（n+1）÷2”个。

当抽象的“数”化作具体的“形”，复杂的数学问题也就不难了。

2. “数”的无穷让“形”的想象无边界。再怎么画，“形”总是有限的，“数”却是无穷的。用“数”表“形”，则形也变得无边无界，可以表示同类问题的所有情况。如下图，在“数”的加持下，这样的形千变万化，可以表示任意一个奇数列的最后一项。既使学生突破了图形想象的边界，又深入理解了“（末项+1）÷2”的道理所在。

3. “数”“形”结合让难题解决更简单。在后续练习中，关于图形中“最外围”的“数”的问题，一旦把它转化为“面积差”来理解就非常容易了：

它们都可以用“整体面积”减去“内部面积”。并且通过算式的代数整理（如第2题）得到最简形式：当有n个绿色小正方形时，蓝色小正方形的个数为“3（n+2）-n=2n+6”。在“数”的解析下，“形”的特征也更显著。

“数”与“形”，如鸟之双翼，车之两轮。执其一端，则不行；并行不悖，则畅通。

【注：本文系2022年度云南省教育科学规划项目“基于核心素养的小学生推理意识培养的策略研究”（批号：BFJC22020）阶段性研究成果】