“几倍”不是“几个几”

“倍的认识”是人教版三年级上册第五单元的内容。可以说，“倍”的认识是小学阶段“数概念”思维水平的一次重要提升，它使数从表示具体的“量”上升为表示抽象的“率”。建立好“倍”的概念，将为后续学习“零点几倍”“几分之几”“百分之几”打下坚实的基础。

现实教学中，大部分老师把“几倍”与“几个几”等同起来，客观上降低了学生的思维难度。但“几倍”与“几个几”是完全相同的概念吗？这恐怕值得商榷。

一、“几倍”与“几个几”的联系

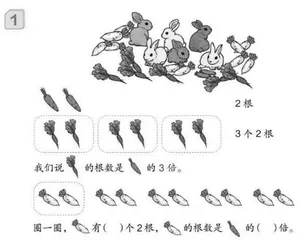
关于三年级“倍的认识”这节课的教学，很多教师觉得完全不费吹灰之力就能让学生掌握，只要把之前乘法学习中的“几个几”学好了，在这里换个说法就是“几倍”。教材的编排也是在学生学习了乘法和除法的基础上来学习“倍的认识”，通过借助“几个几”来降低学习的难度。（如下图）

教学时，老师们通常先对萝卜进行分类计数——红萝卜有6根，胡萝卜有2根；再通过圈图、比较得出“胡萝卜是1个2根，红萝卜是3个2根，我们就说红萝卜是胡萝卜的3倍”。在此基础上，学生很快就能迁移得到“白萝卜有5个2根，白萝卜就是胡萝卜的5倍”。至此，大部分同学都会表示萝卜间的倍数关系了，这时教师只要再通过几道变式练习强化一下“几个几”和“几倍”的联系，就能让几乎全班同学在各类习题中顺利过关。

用“几个几”来理解“几倍”，既体现了知识的正向迁移价值，又提高了学习效率，似乎是一个不错的办法。但有的学生在判断上图红萝卜的根数是胡萝卜的几倍的时候，把两根胡萝卜也看作“1个2”，这样就一共有“4个2”，从而得出“红萝卜的根数是胡萝卜的4倍”这样的错误结论——因为在学生初次学习乘法意义“几个几”的时候，都是从“第一份”数起的，在学习“几倍”的时候，也会自然而然地把原来学习的经验“迁移”到这节课中。

由此可见，“几倍”就是“几个几”的理解方法似乎存在思维上的漏洞。

二、“几倍”与“几个几”的区别

从最浅显的生活经验可以想得到，“几倍”与“几个几”还是有着本质的区别的，具体的比较结果如下表：

由上表可见，“几倍”与“几个几”有着本质的区别。用“几个几”来理解“几倍”，表面上看似充分发挥了旧知识向新知识的迁移作用，提高了所谓的课堂教学效率。但却因言害意，降低了学生的思维水平，难以深入理解“倍”的概念本质。

三、深入理解“几倍”的实践探索

深入理解“倍”的本质，需要循序渐进、展开推理、逐步抽象，形成一个完整的思维闭环。

1. 明确“倍”是比出来的

“几个几”是“数”（shǔ）出来的，而“几倍”是“比”出来的。它描述的是两个量之间的比较结果——而这种比较不同于一年级所学的“相差数量比”（其结果是一个具体的相差量），而是一种“包含份数比”（其结果是较大数包含几份相当于较小数的量）。“几个几”在视觉上是由几个零散的“部件”组成一个更大的“群体”，而“几倍”在视觉上是用较小的一个数作为“尺子”去度量一个更大的“对象”。

教学中，老师可以通过圈一圈、数一数的方式，让学生逐步明白“倍”是比出来的——它是两个量之间的关系，所以不能单独说某个数是“几倍”。再通过PPT动画演示，发现每比较一次都是“尺子”与“对象”的一部分“重合”，所以在描述“几倍”的时候，不包括“尺子”（一倍数）。（如下图）

2. “一倍数”是认识“倍”的根本

同样是红萝卜和胡萝卜做比较，6根红萝卜是2根胡萝卜的3倍，6根红萝卜是3根胡萝卜的2倍。红萝卜的根数并没有发生变化，变化的是“一倍数”，一倍数是“几”，就要用这样的“标准”到对象中去“度量”，度量得几次，就说对象是标准的“几倍”。（如下图）

纵向来看，同样是得到了“2倍”。6根红萝卜是3根胡萝卜的2倍，8根白萝卜是4根胡萝卜的2倍。都是把胡萝卜的数量看成一倍数去度量，在红萝卜或白萝卜中都分别度量得两次，所以倍数都是2。不难发现，倍数是几，其实和具体的萝卜数量无关，只和“度量”得到的次数有关。

所以说，“几倍”是从“一倍”开始的，“一倍”的标准是什么样的，就按照这样的标准在较大数中“一倍”“一倍”地比下去。“一倍数”是认识“几倍”的根本。

3. “倍数”学习中的“变”与“不变”

在上面的例子中，“一倍数”不变的情况下，在越大的对象中比出来的倍数就越多，反之则越少。在对象相同的情况下，“一倍数”（尺子）越大比出来的倍数就越少，反之则越多。

6根红萝卜是2根胡萝卜的3倍，8根白萝卜是2根胡萝卜的4倍，“一倍数”不变——都是2，测量的对象变大了，测得的倍数也就多；而当对象不变都是8时，一倍数是2，能比出4倍，一倍数是4时，就只能比出2倍了。

但也有不变的情况。就是当“一倍数”和对象都按照相同的倍数扩大或缩小的时候，比出来的倍数是相同的。（如下图）

8根白萝卜是2根胡萝卜的4倍，当胡萝卜和白萝卜的数量都增加到原来的2倍时，16根白萝卜仍然是4根胡萝卜的4倍，倍数不变——用“大尺子”测量“大对象”与“小尺子”测量“小对象”，得到的结果相同。

通过“变”与“不变”的操作、观察与思考，学生终于体会到“倍”是两个数相比得到的一种抽象的关系（率），与具体的数量没有关系。

四、“几倍”在生活中的实际应用

学习这么抽象的“倍”，有什么用呢？用途大致有三：

其一，简化数量关系。比如某位打字员录入1500字的文稿需要11分钟，他以同样的速度录入3000字的稿件需要多少分钟？因为第二份稿件的字数是第一份稿件的两倍，第二次的耗时自然也是第一次的两倍，所以需要22分钟。

其二，揭示某种规律。比如在配置糖水的时候，水的数量与糖的数量相比得出的“倍数”其实意味着糖水的甜度。无论糖与水的具体数量如何，只要“倍数”相同则两杯糖水的甜度相同。

其三，奠基后续学习。较大数与较小数相比的结果是一个“倍数”（强比）；较小数与较大数相比的结果是一个“分率”（弱比）。它们形式不同，本质相通。对“倍”的本质意义理解到位了，“分率”的意义理解，也就是水到渠成之事。

由此可见，“几倍”不是“几个几”，值得我们下大功夫引导学生理解其本质含义。

【注：本文系2022年度云南省教育科学规划项目“基于核心素养的小学生推理意识培养的策略研究”（批号：BFJC22020）阶段性研究成果】