培养学生数学“量感”的几种路径

《义务教育数学课程标准（2022年版）》指出：量感主要是指对事物的可测量属性及大小关系的直观感知，是通过视觉、触觉等多种感官对物体的大小、多少、轻重、厚薄等的感性认识。量感的形成可以通过直观感知、测度体验、测算提升等几个层次的活动来实现。那么，教学中如何培养学生的“量感”？笔者以“认识周长”教学为例，谈谈培养学生“量感”的一些方法。

一、在画中感知“量”

感量操作是学生“量感”建立的基石。“对‘单位量’的感受与体验及“对‘累计量’的感受与体验”是感量的两种形式。“单位量”重在引导学生建立“标准”，“累计量”旨在让学生对于“大小”“多少”“快慢”等从模糊的定性到精准的定量的提升。“认识周长”这节课承载着培养学生量感及对“累计量”精准定量。

如，在教学“认识周长”一课时，基于学生的生活经验，选择学生最为熟悉的“400米比赛”作为导入，动态演示学生跑400米的过程，学生充分调动自己的视觉、听觉等多种感官，在“观—思—悟”中准确判断出：从起点出发绕着操场的边线一圈回到起点就是操场的一周；“起点”可以是边线上的任意一点，只要能绕着边线一圈“回到这一个起点”就是这个操场的一周，明确“一周”的概念。在实景操作的基础上，教师还设计“动手描一描”活动，引导学生在图形上找一周，从具象到抽象过渡。

这种从“直观表象”到“抽象表象”的过程中，学生有效建立“单位量”的表象，也为建构“累加量”埋下伏笔。

二、在量中体验“量”

“周长”本质是长度单位的累加。学生能够感知基本的长度单位并理解概念背后的本质是度量。史宁中教授曾指出：度量是数学的本质，是人创造出来的认识数学进而认识现实世界的工具；度量的本质在于对事物的某些指标进行量化，以及对量化顺序的感知。如，在教学“认识周长”一课时，我们着重从以下三方面入手，增强学生量感素养。

（一）实践操作，体验量感

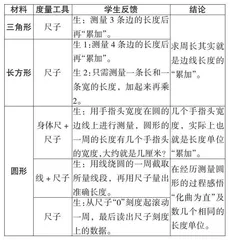
亲历度量过程，直观体验事物的可测量属性及大小，是培养学生量感的必要环节。教师应注重引导学生经历量感学习的观察、体验和顿悟过程，提供可视的探究活动；再通过实验、推理、比较、联想等策略，引领学生建立量感、精准量感，让量感学习真实可见。三年级的学生已经有了“度量”的经验，在此基础上设计“动手量一量”的活动，给每个小组提供丰富的感性材料（三角形、长方形、圆形）引导小组合作探究。

学生通过动手量直边的图形感知直边图形的周长是“线累加”的过程，在经历操作测量曲边图形的过程，感悟“化曲为直”的思想。学生在操作中不仅合理估计培养估算意识，同时在探索中发展了量感。

（二）引导交流，强化量感

“周长”本质的理解，它需要学生经历“读取信息—加工信息—表达想法”，即从直观到抽象的过程。教学时，教师将上述三种图形的一周全部取下贴到黑板上，原来“曲的、不规则的、几条线段”，经过“化曲为直”“长度累加”具象变成一条看得到、摸得着的“直线”，而学生在观察中会发现周长的本质就是“线的长度”，求图形的周长就是把图形每一条边线的长度累加起来的过程。学生在个性化的实践和探究中丰富了“感量”经验，同时也促进了量感的形成和提升。

（三）联系生活，强化量感

1. 找准“累计量”。周长是单位长度的累加，为了精准量感，首先应找准“累计量”。为了强化学生对“周长”这一概念的认知，笔者先设计了“五角星”（如图1），并对学生提问：“下列哪个选项所示是五角星的周长？”

生1：选A，因为五角星上的线都是它的周长。

生2：选B，因为周长是指“封闭图形的边线一周的长度”，只跟“边线”有关，跟其他的线没有关系。

作为感知素材，学生必须先突破“线”这个枷锁找出正确的“累计量”。现实问题和原有经验的碰撞，能让学生在活动中引发自我反思和培养批判精神，使学生在教师的引导和自我的内化过程中，获得解决新问题的经验，实现经验由低层次向高层次的丰富和升华。通过辨析，学生进一步明晰核心概念“周长即是特殊线段的长度”。

2. 找准“长度量”。“线”与“面”二者同时存在于图形中，“面”于视觉效果而言是更清晰的感知，而“线”是一条弯弯绕绕不易察觉的存在。所以笔者将“面”这一极为容易混淆的概念引入设计了“创图形”的活动。

活动内容：用这一条线创造一个有周长的图形。

问：这些图形的周长相等吗？

生1：不相等。图形比较大的周长大，图形比较小的周长小。

追问：图形比较大指的是什么大？

生1：面比较大。

生2：不管围成的是什么图形，它们都是用“同样长”的线段围成，所以周长一定相等。

学生的视觉感知带给了他们一种错误的认知：面大周长就长，面小周长就短。应从周长的本质出发：度量这些不同图形的周长就是在度量这些图形“一周”的长度，而它们的“一周”都是“同样长”的一条线即它们的周长相等。巩固周长概念的内涵，发展概念的外延，面的大小对周长的长短是没有影响的，学生在度量之前应先明确度量的对象，这一环节的设计目的是引导学生从概念本义上理解“长度量”的特征，学生能深刻理解周长含义，学生的量感再次得到发展。

三、在比中辨析“量”

对于学生来说直观形象是他们的认知特点，学生在计算图形的周长时最直接的方法是线段的累加。当学生进行两个图形的周长对比时，通常采用两种思辨方法“合”与“分”。先“量”再“加”后进行比较即是“合”的过程；通过“观察—猜测—推理”后进行“平移”再“比较”即是“分”的过程。在“对比周长”的过程中不仅培养了学生的观察能力，还发展了学生的推理意识。笔者提供了两个图形（如图2和3），供学生对比探究。

首先，找图3的“一周”在哪里，而后采用不同的方法进行思考。方法一：采用“合”的思维进行比较，即先量出“一周”中各条线段的长度再把它们加起来；方法二：采用“分”的思维进行比较，即通过“平移”将两个不同的图形改变至有更多相同属性的图形后再比较，也就是图形对应边的长度相等，图形的周长就相等。

其次，为了内化学生对周长的认知，出示图4并追问：现在图4这个图形变得很细很细了，周长还会一样吗？在视觉上给学生制造一个更大的冲击，如果这个面变得很小很小呢？引导学生思考，还能通过平移得到对比结果吗？学生在这一环节中经过了图形变式导致认知矛盾的产生，再到方法渗透改变图形从而达到认知矛盾化解，最终得到对比结果。学生在这一感性对比的过程中获得了理性的认识，量感得到了进一步培养。

最后，出示“凹”“凸”（如图5）这两个图形的周长对比，学生有了“分”的思维概念后，通过平移改变图形的形状再对比。操作前猜测平移后可以得到两个一样的长方形，他分析的依据是，一个是向下多了3条线段，一个是向上多了3条线段，两个图形多出来的3条线段又是一样的。动手操作后发现：“凹”的周长比“凸”的周长更长，平移后“凸”字正好能变成一个长方形，而“凹”字平移成一样大的长方形后还多了两条边。学生的学习状态不能止于“形式把握”，而是将知识的内在本质联系起来，引导学生学以致用，同时善于猜想、观察、实践，并最终得出结论，培养了学生的推理能力，发展了量感。