基于思维进阶的高中地理跨学科主题学习方案设计与实践

学生在学习过程中如何将获取知识、发展能力和形成态度完美结合，采用项目化学习的方式是一条有效途径，本文通过“学校所在地地理坐标测定”的方案设计与实践，进而引领学生进行深度学习，让学习真实发生。

一、理念与思路

项目化学习作为当前国际上所倡导的一种全新的学习形态，为创造力的培养提供了新的实施路径。“学校所在地地理纬度的测定”方案设计与实践的项目化学习过程的开展，立足于真实的情境创设，让学生在学习任务完成与讨论的过程中，提升学生发现问题、分析问题和解决问题的思维能力。整个项目化学习的过程由浅入深、层层递进。为此，可以分四个逐步进阶的思维层级完成。

1.以合理的情境创设为深度学习奠基

高中地理选择性必修一关于“地球运动的地理意义”的相关知识的学习，是整个高中地理学习中让学生普遍感觉较为枯燥且抽象的内容。开展“地理坐标测定”学习活动，主要目的是强化学生对于太阳视运动的变化、时差和太阳高度的变化等相关知识的理解和运用能力。因此，增强学生的学习兴趣以及化难为易的教学思路就显得尤为重要。为了达到这方面的效果，笔者刻意选择了“校园”这一学生极为熟悉的地点，围绕学生学习与活动的校园环境组织教学，激发了学生的求知欲，让学生在真实的生活情境中去发现、去思考、去总结，成为学习活动取得成功的重要保障。同时，通过在“校园”中进行探究，在总结与提升中以点带面，也有利于学生举一反三，将相关原理和方法进行迁移运用。

2.以思维品质的提升为深度学习铸魂

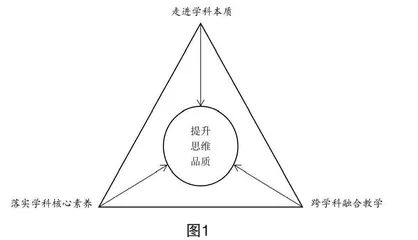
根据《普通高中地理课程标准》（2017年版2020年修订）（以下简称“课程标准”）的要求，笔者提出“一核心三途径”的理念（图1），以“学校所在地地理坐标测定”为案例，带领学生进行测量方案的设计，并进行教学实践。

一核心：提升思维品质。新课程改革要求教学要从教会学生“解题”到“解决问题”，教学中就要注重学生思维品质的提升，关注学生体验，让学生学会在真实的情境中学会发现问题、分析问题和解决问题，从而解决学生深度学习过程中的“痛点”和“难点”。本文通过带领学生按照“方法探究—具体实践—反思总结”的逻辑主线进行学习，有效地促进学生学习过程中思维水平的培养和提升。

三途径：

（1）走进学科本质。课程标准指出：“地理学是研究地理环境以及人类活动与地理环境关系的科学，具有综合性和区域性等特点。”“人地关系是地理学研究的核心主题。”通过带领学生在户外进行实地测量，通过测量点的选择和误差分析等过程，让学生真真切切地体会到人类活动受到自然地理环境的影响，从而清楚地认识到必须协调好人类活动与地理环境的关系。

（2）落实学科核心素养。在以“学校所在地地理坐标测定”为主题的系列学习过程中，通过设计力、动手力、计算力、反思力和交往力“五力”的具体落实有效培养学生的地理实践力：指导学生亲自进行测量方案的设计有效培养他们的“设计力”；对于不同的测量进行测量实践培养学生的“动手力”；对于测量数据的统计与分析等培养学生的“计算力”；对测量的误差进行反思并寻求解决方案培养学生的“反思力”；整个测量过程中与老师和同学的沟通与协作培养学生的“交往力”。

（3）跨学科融合教学。随着各种新兴学科和交叉学科的发展，跨学科融合已成为基础教育的重要任务。有效的跨学科融合可以促进学生对所学知识的深层次理解，促进学生深度学习。对于“学校所在地地理坐标测定”这一内容的学习，学生自制测量器材，通过测量、记录、统计和计算等学习过程，在立足地理学科特色的同时，很好地和数学、物理等学科进行有效融合，并实现五育融合，提升了学生的劳动素养。

总之，通过带领学生进行“学校所在地地理坐标测定”的方案设计与实践，在走进学科本质、将学科核心素养落地和开展跨学科融合教学的体验中，很好地培养了学生的思维能力，利于学生对于地理问题的理解和领悟，从而促进学生学习的进阶。

3.以层级学习进阶为深度学习增色

学习进阶注重的也是学生对概念的逐级发展，强调教学中要遵循学生的认知发展水平，并且要关注学生原有知识水平即已有图式。“学校所在地地理坐标测定”的方案设计与实践，通过对学生四个思维层级（图2）的培养，促进学生认知水平的发展，逐级加深对相关问题的认识和理解。

二、方案与实践

1.第一层级思维：文献研究与方法探究

（1）设计目的：本层级旨在通过创新作业的设计与实施，让学生在文献检索的基础上，结合所学知识根据自身理解设计出合理的方案。这是一个引导学生将所学知识进行内化和灵活运用的过程，同时把方案的构思与解决实际问题相结合，整个过程有效培养了学生的地理实践力。

（2）创新作业：设计一个实践活动，测定学校所在地的地理纬度。

①要求：新颖独特，具有可操作性。

②内容：所需器材具有普遍性，写出具体操作步骤，简要说明所设计方案的优点和不足。

（3）实践反思

高中地理教学中地球运动的相关知识对学生来说理解难度本身就很大。可以以创新作业的形式让学生自行设计方案，这一方面充分调动了学生学习的主动性，在主动探究的过程中加深对所学知识的理解；另一方面学生自主设计测量方案，在教学实际中强化了对地理实践力的培养。实践证明，这样的形式取得了很好的效果。实施下来，虽然很多同学上交的都是现成的经典方案（即下文“第二层级思维”中的方案），但过程中通过文献检索培养的学习能力在高中阶段是难能可贵的。同时，也有的同学上交了一些自行设计的创造性方案，很好地培养了学生的创新思维能力，下文“第四层级思维”中的方案即是笔者把学生自行设计的方案优化完善后再次带领学生运用于实践的尝试。

2.第二层级思维：晴朗天气一天中多次测量取正午数据计算

（1）设计目的：通过指导学生对经典方法“立竿见影法”的领悟与实践，强化对选择性必修一所学到的地球自转的地理意义（地方时的计算）和地球公转的地理意义（正午太阳高度的计算）相关知识的运用，理论联系实际，提高学以致用的能力。

（2）具体方案

所需器材：杆（1.5米左右），三角函数表，皮尺，三角板，粉笔等。

操作步骤：

第一步，先测出杆长。在一天的正午前后分别取几个时间点，进行测量，即时进行记录。

第二步，通过测量数据对比，取杆影最短的一组数据，由所学知识可知当地地方时为12时。

第三步，根据已知条件运用地方时的计算方法推算出当地的经度。

第四步，设正午太阳高度为H，杆长为a，正午影长为b。根据tanH=a/b，通过计算，由三角函数表查出正午太阳高度。

第五步，由公式H=90°-纬度差，推算出纬度差，进一步得出测量地所处纬度。

第六步，组合经度、纬度得出测量地经纬度。

（3）实践反思

该方案在实际操作过程中，受到杆与地面垂直程度等因素的影响，实际测算结果与理论数据会存在一定误差。尽管在实践过程中采取措施尽可能优化测量与计算的过程，但误差是无法避免的。这就让学生充分认识到理论和实践的差距，从而认识到走进真实的现实世界验证所学知识，增强对所学知识的深度理解和领悟的重要性。

3.第三层级思维：取晴朗天气一天中任意时刻测量的数据计算

（1）设计目的：从晴天测量取正午时刻的数据计算到取任意时刻的数据计算，是学生在思维认知上的巨大跨越。这样的思路有利于打破定式思维对学生的束缚，让学生能开阔思维，多角度看问题，很好地培养学生的创新思维能力。

（2）具体方案

所需器材：皮尺，杆（1.5-2米），彩色胶布或丝带，量角器，三角函数表，指南针，计算器。

操作步骤：

第一步，找准测量点，用指南针确定正北方向。

第二步，测量杆长和影长（每次测量时，将杆影轨迹在地面上画出），算出太阳高度。

第三步，根据影长相对于正北方向的变化，判断测量时，当地正处于（“上午”或“下午”）。第一次测量，用量角器量出此时杆影偏离正北方向的角度为     。

第四步，计算出测量当日太阳直射点的纬度δ为 。

第五步，第一次测量时太阳时角t1为     ；第二次测量时太阳时角t2为     。

知识介绍：规定正午太阳时角为0，上午时角为负值，下午时角为正值。每小时对应的时角为15°。

第六步：联立任意时刻太阳高度的计算公式sinh=sinφsinδ+cosφcosδcost，计算出测量地的纬度为    。

sinh1=sinφsinδ+cosφcosδcost1

Sinh2=sinφsinδ+cosφcosδcost2

第七步：通过测算得出，学校所在地的地理坐标为

，       。

（3）实践反思

该方案在具体实践中，也存在一定的误差，通过带领学生进行分析和讨论，得出产生误差的原因主要有四个方面：

正北方向的寻找、杆的粗细的选取、测量仪器的精度。计算时取用的三角函数本身就是近似值，在启发学生探索误差减小的过程中，对学生科学探索思维和能力的培养起到了作用。

4.第四层级思维：不依赖日影进行测量与计算

（1）设计目的：该思路进一步打破了学生的传统认知，在不依赖日影进行测量的思路下，进一步拓展了学生的思维，要求学生需要具备很高的创造性思维能力。无论是从实验器材的制作，还是到具体测量数据的记录，以及对测算结果的论证，都是对学生思维的进一步延伸。

（2）实践方案

所需器材：重球、挡板、秒表、米尺、计算器、三角函数表、复写纸等

理论依据：

第一，θ=15°×t×sinφ【θ为物体偏转角度，t为偏转所用时间（单位取“时”），φ为当地纬度】。

第二，北半球地表作水平运动的物体向右偏转。

操作步骤：

（提前准备）

第一步，在挡板贴一层白纸，在白纸表面再贴一层复写纸。（挡板受到撞击后，会在白纸上留下一个小圆点，便于最后测量。）

第二步，在球运动平面的起始点和终点之间确定一条直线a（以下简称控制线，同时也是表示重球的初始运动方向），用彩色胶带固定。（便于固定每次测量时的参考点，减小误差。）

第三步，量出a的长度为     。（单位：米）

第四步，在放挡板的位置做一条线与控制线a垂直，用与挡板长度一致的彩色胶带进行粘贴标注（挡板受撞击后难免会移动距离，便于下次测量时迅速恢复位置，减小每次测量误差），并在挡板与控制线a垂直相交的位置做一条线b与地面垂直。（实验要测量重球和挡板每一次撞击的点与b线的垂直距离c用于计算）

课堂操作：

第一步，斜坡凹槽对准控制线，并尽量保证与控制线在同一个平面上。

第二步，从斜坡上释放重球。

第三步，当重球即将进入平面时开始计时（重球运动速度快，若看到球到了平面再计时，人需要一定的反应时间，最终会导致所计量的时间变短），当看到球即将接触挡板时停止计时，所花时间记录为t。

第四步，反复测量数次。

第五步，量取挡板每一次撞击的点与b线的垂直距离c。最终完成下表。

第六步，选取最满意的一次测量，进行如下计算。

第七步，由tanθ=c/a，求出tanθ=   ，然后查三角函数表得到θ为（  ）°（  ）′。