指向深度教学的初中数学课堂策略探究

摘   要：深度教学是针对浅层学习局限的教学活动，实施深度教学是全面深化教学改革、落实核心素养的重要路径。采用精准诊断学情；设置问题链；挖掘知识内在结构；深化反思，促进高阶思维的形成四项措施来开展深度教学，促进学生数学核心素养的发展。

关键词：初中数学；深度教学；课堂设计；教学策略；核心素养

中图分类号：G633.6    文献标识码：A    文章编号：1009-010X（2024）05-0036-03

数学课程是数学学科落实“立德树人”根本任务的重要载体，目标是培养学生的数学核心素养，而深度教学是实现这一目标的重要途径。深度教学是基于知识的内在结构，通过对知识完整深刻的处理，引导学生从符号学习走向学科思想和意义系统的理解和掌握，并导向学科素养的教学。结合冀教版“等腰三角形的性质”课例，探讨初中数学深度教学策略。

一、深度教学的研究现状

1956年布鲁姆的《教育目标分类学》中体现了浅层学习和深度学习思想。1976年马顿等首次提出深度学习概念，直到艾根的研究实现了从深度学习到深度教学的转向。2006年郭元祥教授首次提出深度教学的理论和改革实践探究。2017年李松林教授归纳了深度教学的基本范式。2018年刘月霞等阐述了深度学习的定义，实现深度学习的条件路径。前人的研究丰富了深度教学理论，还有一些教师在促进思维进阶、基于学业评价等方面开展了初中数学深度教学探究。

二、基于核心素养的深度教学理论分析

（一）核心素养与深度教学

《义务教育数学课程标准（2022年版）》（以下简称《课标》）明确提出发展学生的数学核心素养。教师作为深度教学实施者，要落实数学核心素养的培养要求，必须明晰核心素养的目标导向，深入把握内在要求和培养目标，始终把发展学生数学学科核心素养作为核心任务。数学深度教学是以情境为背景，以体验、探究为依托，关注学生学习过程、思维发展过程、正确价值观形成过程的教学活动，与核心素养的指向一致。

（二）深度教学理论基础

建构主义理论强调以学生为中心，重视学生在教学中的主体地位，发挥教师的引导作用，从而实现对知识的深度理解，与深度教学所倡导的为理解而教相契合。多元智能理论更重视后天影响，坚信只要教育方法科学，每个学生的智力都能得到发展，这也符合数学深度教学的要求。

（三）深度教学的要素分析

教与学是双边活动，深度学习离不开深度教学，深度教学的关键是学生的深度学习，深度学习的本质是指向学生素养形成的有效学习。核心素养引领下的深度教学基本要素一般包括：创设情境、自主探究、巩固与应用、总结反思、迁移拓展。这些要素与培养学生思维能力、提高学习动机、素养的形成有密切联系。

三、初中数学课堂深度教学策略

郭元祥教授说深度教学是意义性教学，是为理解、生成而教的教学。初中数学深度教学应以真实情境为学习载体，以具有高阶思维导向的问题为引导，以深度探究活动为重要方式，以反思总结获得深度提升，引导学生进行深度学习，发展应用意识和创新意识。因此，教师应当采用深度教学策略，引领学生进行深度学习以培养数学核心素养。

（一）精准诊断学情，创设真实情境

学情包括学生的身体、心理、智力、情感等方面的发展情况及学习情况。精准诊断学情后，教师通过创设合理的真实情境，搭建起数学知识与旧知识或生活实际的桥梁，激发学生的学习兴趣，发现思维的起点，使学生高认知、高参与地卷入到数学活动中来，引导学生学会用数学的眼光观察现实世界。

案例：创设等腰三角形的性质情境

温故：在小学四年级我们已经初步认识了三角形，在七年级进一步研究了三角形的相关概念，本节课研究一种特殊的三角形—等腰三角形。

情境：2008年通车的港珠澳大桥上也有它的身影。港珠澳大桥是世界上最长的跨海大桥，是世界桥梁史上的巅峰之作。我们一起欣赏这些美丽的等腰三角形（出示图片）。

教学分析：从学生的最近发展区出发设计问题，符合学生的认知规律。展示与港珠澳大桥有关的含有等腰三角形的图片，契合时代特色，能引起学生学习数学的兴趣，激发学生民族自豪感，引发学生的深度学习。

（二）设置问题链，实现深度自主探究

设置问题链引导学生找到思考数学问题的本质和关键点，培养他们分析和解决问题的能力。通过提问、讨论和分组活动等方式激活学生的思维，让学生在探究中层层深入思考，寻找到思维的方向，实现深度自主探究。

案例：等腰三角形的性质自主探究环节

问题1：请同学们画一个等腰三角形，并说明为什么它是一个等腰三角形（学生画图）？

教学分析：同学们独立画一个等腰三角形，既是对等腰三角形定义的深化，又为后续性质的研究提供了丰富的图形基础，发现思维的起点。

问题2：观察画出的等腰三角形，你想研究等腰三角形哪些方面的问题？研究它们的什么关系？

教学分析：提出开放性的问题，提升学生猜想探究的思维意识。类比三角形和平行线的研究方法，让学生明确探究的内容为图形的对称性、边、角、重要线段的关系，从而寻找思维的方向。

问题3：得到猜想后，你能证明它们吗？

猜想1：等腰三角形的两个底角相等。

猜想2：等腰三角形顶角平分线、底边上的中线、底边上的高重合。

教学分析：教师引导学生深度观察、发现、猜想、证明，并归纳出作辅助线构造三角形全等的思路，确定思维的策略。学生在经历性质发现和证明的过程中，提升了合情推理和演绎推理的能力；教师对学生的证明方法进行分析和提炼，教给学生深度思考的角度，使学生不仅知道证明方法是什么，还能理解方法是如何得到的。

（三）挖掘知识的内在结构，让深度学习自然发生

挖掘知识间的逻辑关系，做到完整化、系统化掌握课堂知识。整合教材，引导学生有目的、循序渐进地探索，让学生不仅能运用已有知识和技能解决实际问题，还能在学习过程中构建新的知识体系，形成新的解决问题的思维，达到深度学习的目标。

案例：巩固、应用等腰三角形的性质。

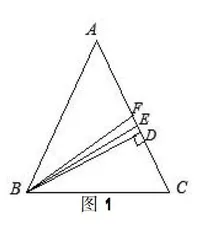
问题4：（如图1）等腰三角形从顶角出发的线段满足“三线合一”，从底角出发的线段满足吗？添加什么条件可以满足“三线合一”的性质？

如果添加一个条件，使底边和腰相等，那么这个三角形是特殊的等腰三角形，它具有等腰三角形的所有性质，还有哪些特殊的性质呢？

已知：在△ABC中（图2），AB=AC=BC.

求证：∠A=∠B=∠C=60°.

教学分析：通过辨析“三线合一”的应用条件，自然引出等边三角形，意在体现一般到特殊的数学研究方法。学生很容易猜想出并证明等边三角形的性质，既巩固了等腰三角形性质定理，又培养了学生的逻辑推理能力，数学深度学习在这一过程中自然发生。

问题5 如果把等边三角形变成等腰三角形，再添加两条角分线，那么等腰三角形两个底角的角平分线有什么样的数量关系呢？

例1，在△ABC中（图3）， AB=AC，BD，CE分别为∠ABC，∠ACB的平分线.

求证：BD=CE.

拓展：等腰三角形两腰上的中线相等吗？等腰三角形两腰上的高线相等吗？

教学分析：把等边三角形变为等腰三角形，猜想并证明等腰三角形两底角的平分线是相等的，还可以进一步探究等腰三角形两腰上的高、中线的数量关系，体现由特殊到一般的数学研究方法。进一步培养学生逻辑推理能力，实现学生数学的深度学习。

（四）深化反思，促进高阶思维的形成

反思是学生对自己已有认知的不断思考、重构、生成与创新的过程。引导学生深化反思，把握知识间的内在联系，对所学知识与研究过程获得思维的反思，感受数学的整体性，掌握数学思想方法，以深度反思促进学生的高阶思维的形成。

案例：总结反思等腰三角形的性质

回顾本节课的探究过程，请结合下面三个问题，谈一谈你的感悟与收获。

（1）这节课我们研究了哪些问题？

（2）在研究这些问题时，经历了怎样的过程？

（3）通过这个研究过程，你有什么新的感受和体会？

教学分析：本节课在等腰三角形的深度教学过程中，设计了适度开放、有挑战性的问题和活动，对培养学生数学核心素养与关键能力起着重要的作用，同时展示了一类几何图形特例研究的一般套路，为后续学习平行四边形等内容奠定了基础。在反思环节，学生畅所欲言，在以生为本的民主氛围中培养学生归纳、概括和语言表达能力，接着引导学生回顾探究过程，培养学生独立思考和反思的高阶思维品质，获得思维的反思，促进其数学核心素养的发展，实现数学的深度教学。