情境驱动深度学习 促进核心素养发展
作者: 林森
[摘要]核心素养直接指导、引领教育教学工作,文章首先简述情境与深度学习的基本概念,接着以“函数”的第1 课时教学为例阐述如何基于数学本质创设问题情境,不断优化学生的数学探究活动,驱动学生的数学深度学习,发展学生的数学核心素养.
[关键词]问题情境;深度学习;数学核心素养
《义务教育数学课程标准(2022年版)》(下文称“新课标”) 着重强调“现实的数学”,倡导从学生的经验基础和认知发展水平出发,创设生动活泼的教学情境,培养学生的自主探究能力和合作交流能力,促进学生数学核心素养的发展.基于此,新课标理念下的数学课堂教学常常令人耳目一新,尤其是通过生动活泼的教学情境吸引学生的注意力,激发学生的数学学习兴趣,使学生的深度学习自然发生,数学思维自然生成,核心素养得以发展.
简述情境与深度学习
情境,通俗来说就是具体场合的景象或情景.问题情境是指学习者可以察觉到却无法轻易达到的一种心理困境.深度学习是指在教师的指导下,学生围绕挑战性学习主题展开的有意义的学习.因此,笔者认为教师应站在学生认知发展的前沿,从学生的现状着手,从学生思维的最近发展区出发,有目的地、有意识地创设情境,激发学生的探究欲望,促使学生积极主动且兴趣盎然地研究问题.下面,笔者以“函数”的第1 课时教学为例,具体阐述以情境驱动学生深度学习,促进学生数学核心素养发展的方法和策略,以飨读者.
简析教学过程
1. 情境导入,引发思考
情境创设 教师PPT 课件展示“乌鸦喝水”的图片(图略),引导学生观察图片,并思考从中可以发现哪些数学现象.
设计意图 生活与数学息息相关,数学因生活充满活力,生活因数学充满张力,生活情境的创设可以让数学课堂富有灵动性,释放独特的魅力.在课堂导入环节,教师创设故事情境,能让学生在上课伊始就感知数学知识与生活的联系,从而主动提取脑海中储存的“资料”,展开数学思考,形成初步体验,为后续的深度学习打下坚实基础.
2. 深度探究,体验新知
探究1 关于常量与变量
(1) 一动车以200千米/小时的速度匀速地从甲地驶往乙地,若路程为s 千米,行驶时长为t 小时,则行驶中不变的量及不断变化的量各有哪些?请在小组讨论之后表达自己的想法.(学生火热讨论后给出观点,即①不变的量:甲地到乙地的路程和该动车的行驶速度;②不断变化的量:该动车行驶的时间t 和已经行驶的路程.)
(2) 从本题中试着归纳常量和变量的概念. (通过分析问题,学生可以归纳得出,动车的行驶速度是不变的,即数学上的常量;动车的行驶时间t 和已经行驶的路程是不断变化的,即数学上的变量. 继而在教师的指导下,学生逐步归纳得出常量与变量的概念.)
(3)一辆小型汽车从A 地开往B地,且A、B 两地相距s 千米,若该汽车以v 千米/小时的速度行驶,则可以t 小时到达B 地.你能说一说题中的变量和常量各是什么吗?(s 是常量,v 和t 是变量.)
(4)谁能试着列举日常生活中的一些变化过程?并阐述其中的常量与变量分别是什么.(学生踊跃表达,不亦乐乎.)
探究2 关于函数关系
(1)表1 呈现的是某市水库蓄水量的变化情况,整个变化过程有变量吗?若有,是哪些?随着水位的不断变化,储水量会变化吗?当水位取一个固定值时,对应的蓄水量也有确定取值吗?(学生自主展开合作交流,并分享观点.)
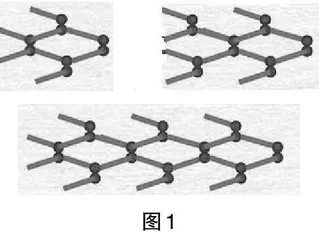
(2)图1 为火柴搭小鱼的示意图,请填写表2,并用含有n 的式子表示S.再进一步思考:模仿(1)中的储水问题,你能对图1 中的火柴搭小鱼提出哪些问题?并作出回答. (学生在填表之后,积极提出问题并解答. 例如,这一过程中是否有变量,是哪些?变量为小鱼的条数n 和所需的火柴根数S……)
(3)观察教材中的“一石激起千层浪”,并用含有x 的式子表示y.(学生很快就能给出正确答案. 之后,教师进一步追问可否用某种方法描述以上两个变量间的关系?学生深度探讨, 并很快有了一致的答案.)
(4)上述水库问题、火柴搭小鱼问题和水波纹问题的变化有共性吗?(在教师的指导下,学生进行了阐述.)
(5)你能总结出函数的概念吗?(在教师的点拨和指导下,学生归纳出了函数的概念.)
(6)上述问题中,变量间存在函数关系吗?谁是谁的函数?自变量是什么?(学生认为,上述三个问题中变量间均存在函数关系,即水库问题中蓄水量是水位高低的函数,其中自变量是水位……)
设计意图 拾级而上的探究可以让深度学习自然发生. 在探究2中,教师巧妙地创设生活问题情境和设计探究活动,让学生亲历概念的形成过程,认识常量、变量,感受两个变量之间的关系,感悟代数与函数的内在联系,最终在深度思考、深度探究和深度交流中掌握数学知识,理解相关概念的本质,涵育数学核心素养.
3. 深度拓展,培养思维
基础题:
(1)有一根10厘米长的铁丝,将其围成一个腰长为x厘米、底边为y厘米的等腰三角形,请写出y和x 间的关系式.并说明y 是否为x 的函数,为什么?x 是否为y的函数,为什么?
(2)图2为一个数值转换器,请用含x的代数式表示y.请问y是x的函数吗?为什么?x 是y的函数吗?为什么?
(3)图3为某市一天内某段时间的气温变化图,描述此图表示的是哪两个变量间的关系,并读出2时和10时的温度.请问温度T 是否为时间t 的函数,为什么[1]?
提高题:
(1) 已知圆的周长公式是C=2πr,这里常量和变量分别是什么?
(2) 以下各式中的x 为自变量,那么y是否为x的函数?
①y =3x - 1;
②y =2x2;
③y =- 2/3x;
④y2=2x.拓展题:
请写出图4中y是x的函数的图象序号( )
设计意图 在应用环节中有计划地设计一些合适的问题和情境作为教学的补充,可以让学生在解决问题的过程中收获方法与经验,实现思维的跃升.
4. 充分总结,升华认识
问题1 回顾一节课的学习历程,你经历了什么?习得了什么?又有哪些困惑?
问题2 最后,让我们一起来了解数学史上的函数.早在17世纪,德国数学家莱布尼茨就已经提出了函数的概念,他是这样定义的……
设计意图 自主小结可以促进学生养成良好的总结习惯,也可以深化学生对知识的理解. 在这一环节,数学史的融入,可使学生更加理解数学、喜欢数学, 进而爱上数学.
思考与感悟
1. 通过关联新知的内容创新情境导入,激发学生深度探究的兴趣
关联新知的内容可以是科技前沿的信息, 也可以是日常生活中的现象, 还可以是学生熟悉的事实. 以关联新知的内容来创新情境导入, 可以充分激发学生深入探究的兴趣, 促进深度学习的自然发生.
2. 借助日常生活的情景设计探究活动,将探究引向更深处
事实上,数学知识与日常生活密切相关,借助日常生活情景设计探究活动,可以让学生对数学知识的学习产生熟悉感,消除内心的恐惧和不自信,使新知有序铺开,进而将探究引向更深处.
3. 精心设计符合学情的创新作业,促进更高效率的数学建构
一些教师的课堂练习受限于教材与教辅资料,这直接导致了学生的高阶思维难以得到有效发展.倘若教师能将教学内容与学生生活情境有效融合,精心设计出符合学情的创新作业,则完全可以促使学生进行更高效率的数学建构.
总之,数学课堂需要有效情境的创设来驱动学生进入深度学习,在情境中最大限度地激发学生学习数学的热情,让学生自动自发地深度探究、乐学善思,提升数学核心素养.