基于不同版本教材谈因式分解的数学理解

［摘要］研究者以因式分解为例，对北师大版和人教版初中数学教材进行了对比分析，发现两版教材在设计理念和内容安排上存在一定差异. 研究者分析了《义务教育数学课程标准》对这部分内容设定的教学目标与要求，发现两版教材尽管内容安排不一样，但是目标一致，教学要求也保持一致. 有鉴于此，研究者从学习因式分解的必要性、因式分解关联的知识、因式分解的方法和因式分解的应用四个方面进行了深度解析，加深学生对数学知识结构化的理解.

［关键词］因式分解；数学理解；教材处理

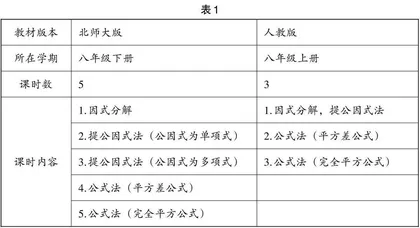
自课改以来，出现了多个版本的数学教材，各版教材特点纷呈，根据不同的编写计划，知识点编排顺序不尽相同，但教材编写的依据无一例外都是《义务教育数学课程标准》（以下简称“课标”） .在课标背景下，教师在教学过程中应与课标的要求保持一致，但他们对数学知识的理解可能影响教学质量，进而影响学生对数学知识的理解与掌握.笔者曾在某重点中学旁听了两节数学课，主题都是“因式分解”，感受颇深. 该校使用的是人教版教材，恰好笔者刚上过北师大版教材的因式分解公开课.为此，笔者将两个版本的教材内容进行了对比，见表1：

从表1可见，两版教材对于因式分解的理解和重视程度不一致.北师大版对从概念的深入认识，到提公因式法的不同处理方法都做了细致处理，而人教版仅仅将因式分解当作整式乘法的逆向变形进行处理，且两个版本课时分配也不一致.一线教师对数学的理解应以课标为纲，从数学本身的要求出发，因为教师对数学知识的理解最终会影响学生对数学知识的理解与掌握.课标对因式分解的要求：能用提公因式法、公式法（直接利用公式不超过两次）进行因式分解（指数为正整数） .“能”的同义词是“掌握”.“掌握”的要求可表述为：多角度地理解和表征数学对象的本质，把对象用于新的情境.掌握的要求比了解和理解

的要求都高，所以无论哪个版本的教材，对因式分解部分的教学要求都应该表述为：

1.对于一个具体的式子，判断其是否可以进行因式分解；

2.能描述因式分解的由来、内涵和特征，能阐述因式分解与整式乘法互逆的过程；

3.理解提公因式法、公式法分解因式的本质，学会利用整体思想将复杂的多项式用提公因式法或公式法进行分解.

学习了整式乘法，可从整式乘法得到多项式，把整式乘法进行逆向变形，由多项式得到因式分解，从操作上来讲并不难.但本节课的课标要求的“能”不仅要求学生会将多项式进行因式分解，还要了解因式分解在整个教学中所处的地位以及对后续学习的影响，这就是学习因式分解的必要性.基于此，笔者从以下几个方面解析“因式分解”这一章节.

学习因式分解的必要性

因式分解在初中阶段代数学习中，对于分式的运算、代数式求值以及方程求解等问题， 起着重要作用.

其次，解决代数式求值的问题时，因式分解能够起到化繁为简的作用. 以a= 136，b=42， 求a² -3ab 的值为例，若计算这个式子的值， 直接代入a，b会使计算过程变得烦琐，如果先对a² - 3ab 进行因式分解， 得到a（a - 3b）， 再将a=136，b= 42代入a（a- 3b） 得136（136-3×42） = 136 ×（136 -126）= 136 ×10，即可轻松得出结果.这表明，因式分解在简化代数式求值问题上颇具实用性.

再者，因式分解法在处理二次或更高次方程、方程组以及不等式时，能有效地起到降次的作用.以求解x² - 5x + 6 = 0 为例， 先将左边的多项式进行因式分解，得到（x -2）（x - 3）= 0，根据每个因式等于零的条件，得到x 的解是2 和3. 因此，因式分解对于解二次方程或高次方程、方程组以及不等式时是有效的工具.

此外，在高中代数学习中，因式分解居于重要地位.通过等式恒等变形对高次多项式进行降次处理，有利于解决函数单调性证明、二次函数极值、零点及参数确定等问题［1］ .

更深层次的原因在于因式分解是一种逆向恒等变形，是发展学生智力、培养数学能力、深化学生逆向思维的良好载体.恒等变形在数学证明中具有重要作用，不仅可以帮助学生理解等式的性质和运算规则，还可以用于推导和证明数学定理.灵活应用恒等变形可以简化复杂的等式，揭示等式背后的数学本质，进而推动数学的发展.欧拉在《无穷分析论》中认为，将整式函数分解成因式，其性质就变得很明显，一眼就可以看出变量取何值时函数值为零.

因式分解关联的知识

事实上，小学阶段已经出现了因式分解的雏形，例如在进行简便运算时有以下题目：

在进行整除判断时，我们还会分解质因数，例如：120 = 2 × 2 ×2 × 3 × 5，可见：120可以被2，3，5整除，也可以被2，2，2，3，5任意组合的乘积整除.由此可得一个数被另一个数整除的方法，即将一个数分解成想要的数的乘积，北师大版教材还提供了如下素材：99² + 99可以被100整除吗？参照上述简便运算法，可得类比数的整除，我们可以提出以下问题：

a²+a可以被a+1整除吗？于是，从数的除法运算过渡到式的除法运算.可见，通过因式分解是判断整除的一种有效途径.

如果无法整除，就自然过渡到了分式表示整式除法运算的结果，这就与数与数相除，无法整除可用分数表示相一致.

如果可以整除，说明a² +a含有a+1的因式，对比分数的约分和通分，可以类似进行分式的约分和通分，为分式的运算打下基础.

所以，因式分解的恒等变形与因数分解的恒等变形的作用一致，这是从数到式的跨越，为式的乘除运算奠定了基础.

因此，从教学设计上体现对因式分解的理解，一定要抓住从数的分解到式的分解的过渡，以及通过数的加减算式中分解出乘积进行简便运算来阐释因式分解转化为乘积的恒等变形的必要性，为学生的思维过渡搭建桥梁.

综上，笔者从学习因式分解的必要性、因式分解关联的知识、因式分解的方法和因式分解的应用四个方面对本节内容进行了深度解析，为本节教学提供了设计思路以及框架.

章建跃教授指出，教师在数学教学过程中要做到“理解数学、理解学生、理解教学、理解技术”［3］ .可以解读为，教师对数学教材的全面理解是提高教学质量的前提. 当教师对教材结构有系统性、整体性的把握时，才能在教学设计中体现知识结构的深度关联，才能使学生学到结构化的、联系紧密的、迁移能力强的知识. 只有把数学知识置于历史、当下和未来社会之下，用联系的、发展的思维去认识、理解、把握、体验和应用数学知识，学生才能真正理解、接受、掌握数学知识的本质，真正把握数学知识的脉络.