“双减”背景下微专题复习课探究

［摘要］微专题复习教学具有见微知著的特点，对于减轻学生课业负担，提升复习效果具有重要作用，这是一种与“双减”政策匹配度相当高的教学模式.实践证明，“双减”背景下微专题复习课需遵循由表及里、以生为本、以素养为纲等原则.研究者以“角平分线”的复习教学为例，从“以点带面，串联知识”“引发联想，解决问题”两个维度展开设计与分析，并从问题驱动与生本理念两个方面谈一些思考.

［关键词］微专题；复习；角平分线

随着“双减”政策的深入推进，学生再也不用辗转于各类补习班或竞赛课了，这不仅真正减轻了家庭教育压力，也让学生有了更多自主学习的时间与空间.但是，值得注意的是，“双减”减的是学习压力与学习负担，而非降低学习质量.将“微专题”教学模式应用于初中数学教学，可有效实现减负增效的目标.因此，这种与“双减”政策目标一致的教学方式，值得广大教育工作者尤其是一线教师去深入探索与研究.那么，在“双减”背景下，“角平分线”的复习教学该如何开展呢？下面，笔者从“以点带面，串联知识”“引发联想，解决问题”两个维度对此问题展开研究.

微专题复习的概述

微专题复习属于一种小型的专题复习课，同时具备“微、专、真”的特点，“微”主要体现在时间短，时长一般控制在20分钟到一节课；“专”主要体现在有很强的针对性，研究对象比较单一，但不局限于某个知识点，也可以是某种思想方法、解题策略、易错点等；“真”体现在“真问题”与“以生为本”等方面，即整个教学活动都以学生的长期可持续发展及核心素养的培养为目标.相较于传统的复习教学，“双减”背景下的微专题复习具有见微知著的特点，对学生个体的发展具有重要推动作用.例如，结合当地中考趋势设定一些专题训练，则能有效挖掘学生潜能，让学生在短时间内高效、深入地理解知识的本质.从某种意义上说，微专题教学有效地提高了学生的复习效果，是落实“双减”政策的教学模式之一.“双减”背景下微专题复习教学的原则

1. 由表及里的原则

传统的复习教学中，教师更多地将目光投射于知识面的覆盖程度上，为了追求复习容量，却忽略了复习的精准度与深度，即使遇到试卷讲评或错题分析，也只是就题论题，学生难以实现真正的深度学习.相较于传统复习，微专题复习并不局限于简单的“对和错”，而是在对错之间铺路搭桥，让学生的思维亲历由浅入深的过程.因此，微专题复习教学需遵循由表及里的原则，结合学生的认知发展规律设计教学活动，推动教学流程，这是提升学力的关键.

2. 以生为本的原则

初中数学知识点既多且杂，这就要求复习教学尽可能地面面俱到，要突出教学的重点与难点，甚至还要关注到一些“既偏又怪”的问题.众所周知，一个人的精力是有限的.既要减轻学生的课业负担，又要保持教学质量不下降，唯有在充分尊

重学生的基础上实施教学，鼓励学生主动提出问题，方能使复习教学的方向更加精准.探索问题时，教师要鼓励学生自主分析、整理与思考，这是完善学生认知体系的基本途径.

3. 以素养为纲的原则

“双减”背景下的微专题复习教学，同样致力于发展学生的数学品质与关键能力.引导学生摆脱“题海战术”是当下亟须解决的现实问题，然而有些教师受传统复习教学思想的影响较深，至今依然沿用过时的机械训练方式，力图让学生接触更多的题型，实现知识面的全覆盖.殊不知，“双减”背景下“立德树人”才是教学的核心目标，只有将促进学生核心素养的发展作为教学的主要任务，才能让学生真正实现知识的融会贯通，获得研究一道题，解决一类题的能力.

教学过程设计

1. 以点带面，串联知识

复习教学如果仍然着眼于概念、定理等零碎型知识点，显然不能满足教学需要.对标中考的复习教学，更需关注知识点之间的联系，要让学生通过复习获得融会贯通的解题能力，提升应用意识.“切口小”是微专题的显著特点，但复习教学却不能局限在某一点上，二者之间是否自相矛盾呢？事实上，“小切口”的目的是将某个点、某一思想方法或错题研究得更加深入、透彻，由此及彼地撬动与之相关的内容是微专题复习的重中之重.因此，二者之间是相辅相成、互相促进的关系.为了提升“角平分线”的复习效果，教师在教学设计环节，就应关注到与角平分线相关的定义、题型与方法等学材，让课堂在以点带面的模式下，向纵深方向发展.

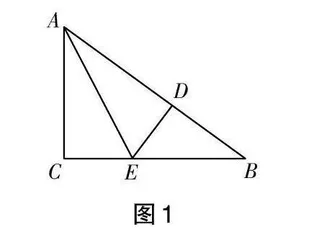
问题1 如图1，已知△ABC中的∠C为直角，若将该三角形以过点A的直线为折痕进行折叠，令点C恰好落在AB边的点D位置，AE为折痕，且AC与BC的长度分别为6和8.根据这些条件，可分别获得哪些线段的长？

在问题1的条件下设计变式1：如图2， 连接CD，与AE相交于点F，根据这些条件，可分别获得哪些线段的长？

变式2： 同样在问题1 的背景下，如图3，过点E 作HE 与CA 平行，所作直线与AB 边相交于点H，根据这些条件，还可以获得哪些线段的长？

设计意图 问题1 是一道简单的角平分线相关问题，不同认知水平的学生都能根据自身已有的认知解决问题.在此基础上，教师有针对性地提出追问与变式，显然遵循了微专题教学由表及里与以生为本的原则.学生通过独立思考、自主探索与交流，不仅发散了思维，回顾了角平分线的性质，还为建构角平分线相关的知识体系奠定了基础. 因此，这样一个以点带面的教学环节，就对知识点的串联起到了铺垫作用，初步唤醒了学生的解题意识.

2. 引发联想，解决问题

联想是指根据一种事物想到与之相关的其他事物的过程，这是一种看不见、摸不着的心理现象.一般情况下，联想存在接近、类似、对比与因果四种情况.纵观近年来各地关于角平分线的中考试题，发现以角平分线为背景命制的考题，考点主要集中在角平分线的性质、等腰三角形、翻折等知识点上.为了充分激发学生的联想力，在教学之初，教师首先应借助丰富的问题与变式启迪学生的思维，让学生自主联想到与之相关的一系列问题，由此总结出与角平分线相关的知识，获得识图能力，为建构完整的知识结构体系服务.通过对上述问题的探索与归纳，教师可在此环节设计以下问题引发学生的联想，进而提高复习效率.

问题2 如图4，已知△ABC中的∠C为直角，其AB，BC 边的长度分别为10 和8，AC 与BC 边上分别有动点D，E，将DE 连接起来.假设CD =x（x＞0），EC=4/3x，把△CDE沿着DE 进行翻折，获得△DEM. 那么，点M 是否有机会处于△ABC 中的某一角平分线上？若有，x值是多少？若无，请说明理由.

学生自主思考过程中，一部分学生提出无法用x 来表示一些线段具体有多长，因为探求不到等量关系，因此无法列方程.为此，教师鼓励学生以小组合作学习的方式进行分析，引导学生从“翻折”这一关键信息出发，逐步完善图4，形成图5，并解构图5中的一些结论.很快，大家发现在隐含信息背景下的DE 与AB 平行，H，M，C三点具有共线的特征.随着师生、生生地积极互动， 最终形成了如下几种解题思路.

解法1 根据“角平分线上的任意点到角的两条边的距离具有相等的关系”来构造基本图形，以图5为基础开始解题. 首先，延长CM与AB 相交于点H，然后过点M 分别作MF 与AC垂直，MG与BC垂直，点F，G 分别为垂足（见图6），易得FM 的值为0.96x，GM的值为1.28x，HM=4.8-1.6x.

如果点M恰好处于∠BCA 的角平分线上，那么FM =GM，0.96x =1.28x，舍掉x=0；

如果点M恰巧处于∠ABC 的角平分线上，那么1.28x =4.8-1.6x，x =5/3；

如果点M恰好处于∠CAB的角平分线上，那么0.96x =4.8 - 1.6x，x =15/8 .

由此可见，当x 的值为5/3或15/8时，点M 处于△ABC的某个角平分线上.

解法2 依然以图5为基础，首先将AM 连接起来形成图7， 若∠CAB 的角平分线为AM，根据条件可证得AC/AH = CM/MH，根据AC，AH，CH的值分别为6，3.6，2.4，可计算出CM 的值为3，根据CM=2OC，可确定OC 的值为1.5，在直角△DOC 中，sin∠EDC = sin∠CAB，因此可求得x的值为15/8 .

解法3 以图7为基础，过点M作MP 与AB 平行，并与AC 边相交于点P，如图8 在AM 为∠CAB 的角平分线时， 可证得PA = PM， 根据CD =x， 能发现MP=1.2x，CP =2x.由此可求得AP 的值为6 - 2x，根据现有条件列方程6-2x=1.2x，解方程可得x 的值为15/8.

解法4 如图9，通过直角坐标系的建立来分析与解决问题（过程略） .

设计意图 一题多解不仅能巩固复习效果，还能进一步发散学生的思维，让学生在联想的基础上厘清知识之间的内在联系，为建构体系化的认知结构作铺垫.在联想的助力下，学生充分发挥想象力，并在独立思考的基础上合作交流，逐步发展推理能力、几何直观、抽象能力等素养.

思考与感悟

1. 问题驱动，精益求精

问题是数学的核心，微专题复习教学同样离不开高质量问题的引领.尤其是在推行结构化单元教学的背景下，遵循“双减”政策，按照“由浅入深，逐层递进”的程序设计问题，可逐步细化知识结构，让学生主动整合与教学内容相关的知识点与资源，为建构完整的知识体系奠定基础.教学过程中，将一些零散的知识点用问题串串联起来，可进一步揭示知识之间的内在联系，便于学生系统化复习，为发展核心素养奠定基础.

纵观本节课的复习教学，教师以一个经典问题作为教学的切入口，通过追问、变式的应用，激发了学生天马行空的想象力，为学生自主探索问题2做好铺垫.从学生应用多种方法解决问题2 的过程来看，整个课堂提出的问题并不多，但每一个问题都处于学生认知的生长点上，一题多解的过程凸显了“少而精”的问题具有大大的能量，整个课堂也在精益求精中拾级而上， 充满活力.

2. 尊重差异，全面发展

“双减”背景下的教学，“学生的学”比“教师的教”更重要，而学生作为学习的主体，客观存在的个体差异不容小觑.在这种背景下设计微专题复习课程，教师应充分了解学情，有针对性地关注每个学生在认知上亟须完善的知识点与技能，只有真正了解了每个学生的优缺点，才能制定出科学、合理的教学目标.新课标的教学目标是：“让人人都能享受到数学教育，让每个人都能在数学教育中获得不同程度的发展.”教学中，教师应针对学生的认知水平与复习课程的特点，在尊重学生的基础上设计层次分明的问题，并逐层递进引导，让学生切实获得减负增效的复习效果.本节课的各个教学环节，教师都将学生放在首位，鼓励或引导学生自主探索与研究问题，必要时加以点拨或鼓励学生合作交流，使不同认知层次的学生都对“角平分线”相关知识有结构化的认识.

总之，关于“双减”背景下微专题复习教学的研究，是一个值得广大教育工作者去探索与思考的话题. 对于中考复习而言，这种教学模式不仅能快速地提升学生的认知水平，还能促进学生个体长期可持续发展.