寻觅图形关联　探求解题路径

［摘要］等腰（边） 三角形在考试中常常作为载体与其他知识相融合，既能考查学生的基础知识与技能，又能提升学生的学科素养. 在教学中，教师应充分挖掘题目的内在数学思想与方法，同时对题目作出一些变式和延伸，让学生既见树木又见森林.

［关键词］等腰三角形；思想方法；拓展延伸

引言

几何试题作为数学检测的重点内容，通常凝聚着命题者的智慧，往往赋予考生更大的发挥空间，通过探究这类题目的多种解法，可以培养学生思维的灵活性；对这些题目进行拓展变式，可以加强知识间的联系，实现学科知识的整体性学习，进而提高学生的解题能力和探究意识.2022年湖北省竹溪县八年级期末考试出现了一道以等腰三角形为背景的几何试题， 通过对全县3000多名学生得分情况的分析，引发了笔者的诸多思考，尤其是对学生丰富的答题思路有了较多了解，进而引发笔者对数学教学工作进行了深度思考与探索.

一题——试题呈现例题

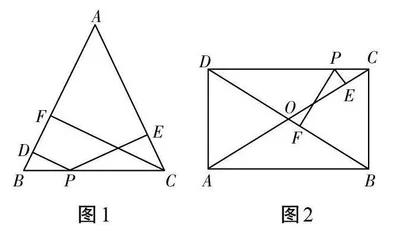
如图1， 在△ABC中，AB=AC，点P 是底边BC 上任意一点，PD⊥AB，PE⊥AC，垂足分别为点D，E，CF⊥AB，垂足为点F.

（1） 试猜想线段PD，PE，CF之间的数量关系，并说明理由；

（2） 如图2，在矩形ABCD 中，AB = 12，BC = 5，点P 是DC 边上一动点，PE ⊥ AC 于点E，PF ⊥ BD 于点F，求PE + PF 的长.

一解——解法探究

本题以特殊几何图形即等腰三角形为背景创设问题，探究其中特殊线段之间的关系，题目设置了两个问题，只要解决了第（1） 问，则可将结论直接运用于第（2） 问.要解决第（1） 问比较简单，题目给出点P 是底边上任意一点，因此可假设点P 恰好处于中点位置；可采用截长法或者补短法，证明三角形全等；也可以采用面积法、翻折法或者相似法来处理［1］ .

1. 特殊位置法

方法1 如图3，假设点P 恰好为等腰三角形底边上的中点，因为AB = AC，PD⊥AB，PE⊥AC， 易证PD =PE. 因为CF⊥AB，且点P为底边上的中点，所以PD 是△FBC的中位线， 所以CF = 2PD=PD+PE.

评注 点P 既然是底边上任意一点，就容易联想到当点P 为等腰三角形底边上的中点这一特殊情况，这就为猜想提供了一种思路，但这个方法仅限于解决填空题或者选择题时适用.