走班制教学对中小学学生学习成效的影响

摘 要

走班制对学生学习成效的影响一直是教育界研究的热点，但不同学者对此有着不同的看法和结论。采用元分析的方法，对国内外34篇实验及准实验研究文献进行了细致分析，旨在从更客观的角度评估走班制教学的有效性及其影响因素。研究结果表明，总体而言，走班制对学生的学习成效产生了中等程度的积极影响。此外，走班制对学生学习成效的影响受到多种因素的调节，包括学段、班级规模、能力分层和学科，而实验周期对其影响不显著。建议在实际教学过程中，应顺应教育改革的趋势，广泛推广走班制。同时，基于学生所在学段和学科的具体情况，选择合适的走班分层教学模式，并重新规划班级规模，以打造更加高效的课堂环境。

关键词

走班制；学习成效；元分析；中小学生

中图分类号G633 文献标识码A  文章编号1005-4634（2025）02-0042-08

走班制作为教学组织形式上的一种创新，融合了分层教学的差异化教育理念和选修制的灵活性，旨在满足学生的个性化发展需求，激发学生的天赋与潜力。这一教学组织形式与最新的高考改革紧密相连，成为改革的关键环节[1]。2019年6月，国务院办公厅发布《关于新时代推进普通高中育人方式改革的指导意见》，强调了适应高中新课程和高考综合改革的必要性，推崇因地制宜、有序实施选课走班[2]。随着时间的推移，走班制的优势进一步显现，进而在中小学阶段也逐渐推广开来，它契合“以学生为中心”的教育理念，已然成为了许多学校招生的亮点。本研究将走班制定义为一种超越传统异质行政班级限制的教学组织形式。在这种模式下，学生可以根据自己的学习水平选择不同的课程，并在同质学习小组中进行学习，以完成各项学习任务。这一定义得到了Judith Ireson[3]、Wikinson[4]、荣维东[5]、李茂菊[6]和余婷婷[7]等多位学者的支持。根据这一定义，走班制的英文表述包括“tracking and ability grouping”或“setting”，这些术语准确反映了其核心特点。

为了验证走班制对于学生学习成效影响的有效性，众多学者展开了大量教学实验研究，但是结论不一，主要有以下三种情况：第一，走班制对于学生的学习成效起着显著的正向作用。胡萍发现高二学生在数学科目上经过半个学期的走班以后学习效果明显提升，学生的课堂效益得到显著提高[8]；Bygren基于学生的GPA成绩发现走班制能够显著促进学生学业成就的发展[9]。第二，走班制对于学生的学习成效没有明显的作用。Preckel在走班制下发现实验组较对照组的学习成绩仅高了约0.43分，影响并不显著[10]；杨超对湘西州A中学学生进行实验研究，发现走班后学生的成绩并没有明显提升，且课堂的学习氛围较弱[11]。第三，走班制对于学生的学习成效起着显著的负向作用。杨文对T中学高中化学走班进行研究，发现教学效果不太理想，现场课堂随意而不可控[12]；Allison在探究setting模式中小学生的阅读能力的发展情况时发现，该模式对于学生的阅读能力存在一定负向影响[13]。因此，系统梳理走班制与学生学习成效相关的定量文献，并且厘清二者产生关系过程中涉及的调节变量的潜在作用，能为走班制的推广、后续的发展走向以及教育管理者如何高效组织实施走班制提供参考。

1 研究设计

1.1 研究方法与工具

元分析由美国教育心理学家Glass提出，是一种应用特定的设计和统计学方法对已有研究进行系统评价和定量分析的方法[14]，本研究以元分析软件Comprehensive Meta-Analysis 3.0（CMA3.0）作为数据分析工具，以森林图、漏斗图及各项效应指标数据呈现最终实验结果。

1.2 研究过程

1.2.1 文献检索

首先在中文数据库进行检索，以“走班制”并含“效果”“影响”“成效”为主题词，使用各文献数据库自带的高级检索功能进行检索，共得到887篇中文文献。在检索英文文献时，分别以“tracking and ability grouping”“setting”并含“achievement”“effect”“outcome”为主题词，在web of science及Google Scholar数据库进行检索，得到英文文献432篇。综上，共检索1 319篇文献，检索时间为2023年11月17日，文献总体时间跨度为1984年至2023年。

1.2.2 文献筛选及纳入标准

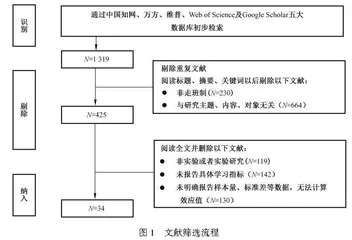
由于文献数量较多，本研究使用Endnote X9进行文献管理并剔除重复数据，随后按照如下标准对纳入文献进行筛选：（1）研究在走班制环境下开展；（2）研究探讨走班制对学生学习效果的影响；（3）研究对象为学生，排除教师、企业员工等群体；（4）研究需明确报告学生学习效果指标（学习成绩或作品评价等）；（5）研究类型属于实验或准实验研究，单组实验需报告前后测数据，双组实验有实验组及对照组；（6）研究中提供了完整的计算效应值的数据，如样本量（N）、平均值（M）、标准差（SD）、t值或p值等。最终，共获得34项符合要求的研究文献样本、86个分析效应值。文献筛选流程见图1。

1.2.3 特征值编码

为了方便后续研究，在进行元分析之前需要对样本文献中的特征值进行编码。不同样本的特征值不同，为了保证编码的准确性和有效性，本次研究由两名编码者分别对这34篇样本文献进行编码，编码一致性达到98%，说明特征值编码的有效性较高。本研究的编码内容包括两个方面：一是文献基本信息，包括文献样本名称、实验组以及对照组成绩平均值、标准差、t值或p值等。为了区分不同的文献样本，将作者（仅第一作者）、出版年份作为编码样本名称，如果一篇文献中的有效数据不止一项，则对应样本名称后用“a”“b”“c”以及“1”“2”“3”进行区分。二是将学习成效当作因变量，将走班制作为自变量。此外，根据纳入的文献样本来看，还存在其他调节变量可能也会对实验结果产生一定影响。因此，借鉴李晓虹[15]47-48、杨冰清[16]、李宝敏[17]等学者对于调节变量的选取，并结合本研究纳入文献样本的共性选取调节变量，编码结果如表1所示（其中实验周期主要根据纳入文献的分布情况并借鉴李晓虹[15]49等学者的调节变量选取情况进行划分）。

1.2.4 元分析框架

本研究按照图2研究框架进行元分析，找到下述问题的答案。

问题1：走班制是否提高了学生的学习成效？

问题2：在走班制背景下，不同的学段、实验周期、学科、能力分层情况、班级规模是否真正对学生的学习成效产生影响？

问题3：调节变量之间如果存在影响，具体哪些维度有益于学生学习成效的提高？

2 研究结果与分析

2.1 发表偏倚检验

偏倚（bias）又称系统误差，指所得研究结果与真实值之间的偏差。在社会科学研究领域中，发表偏倚普遍存在[18]。如果研究中发表偏倚，则说明纳入的文献不足以代表整个相关研究领域的整体状况，估计的效应值也会与实际的效应值大相径庭，进而影响元分析结果的准确性和有效性。因此，本研究采用定性的漏斗图回归方法（Macaskill’s test）及定量的线性回归方法（Egger’s test）来全面评估样本的发表偏倚状况。由图3可以看出，大部分效应量位于漏斗上方，且较为均匀地分散在主轴两侧，初步说明研究存在发表偏倚的可能性较小。而Egger’s秩序检验的结果显示：t=1.93，p＞0.05，进一步说明样本存在发表偏倚的可能性较小，可以对于数据进行进一步的分析。

2.2 异质性检验

通过异质性检验可以确定效应模型的选择，进而判断是否需要后续进行调节变量的分析。异质性检验的方法有很多，本研究拟用Q检验和I2检验判断样本的异质性，进而选择效应模型。Higgins等人研究认为统计量I2＞75%时应选择随机效应模型，0≤I2≤75%时应选择固定效应模型[19]。如果Q值显著则说明样本数据之间存在异质性，应选择随机效应模型。本研究的异质性检验结果为Q=806.31，p＜0.001，统计结果呈现显著水平，说明各样本之间存在异质性；I2=90.57＞75%，说明本研究应该选择随机效应模型。

2.3 走班制对学生学习成效的整体影响

本研究通过计算34项研究的效应值并使用标准化测量作为结果变量，进而得出元分析中走班制对于学生学习成效的整体影响。本研究采用科恩提出的效应值判断标准：当ES＜0.2时，可以认为其影响强度很小；当0.2＜ES＜0.5时，可以认为有中等影响强度；当0.5＜ES＜0.8时，可认为有中上等影响强度；当ES＞0.8时，可以认为有很大影响强度[20]。本研究所计算出来的合并效应值0.772，介于0.5～0.8之间。综上可以认为，走班制对于学生学习成效有着中上等影响强度，能够较为显著地提高学生的学习成效。

2.4 调节变量作用效果的差异与解释

2.4.1 学段对于走班制学习效果的影响

根据研究所纳的34项文献的研究情况，发现样本所涉及的学段主要包括小学、初中、高中三个阶段。由表2可知，其组间效应值Q=14.005，p＜0.05，说明走班制下不同学段的学生学习效果差异显著。不同学段之间的效应作用强度从小到大依次为：初中学段（g=0.242，p＜0.001）＜小学学段（g=0.332，p＜0.05）＜高中（含中职）学段（g=0.473，p＜0.001）。各学段的效应量均处于0.2～0.5之间，说明走班制教学对于各学段学生的学习成效有着中等强度的促进作用。

2.4.2 实验周期对于走班制学习效果的影响

根据纳入研究样本的实验周期情况，不同实验周期的效应作用强度依次为：9周以内（g=0.316，p＜0.001）、9～16周（g=0.403，p＜0.001）、16周以上（g=0.353，p＜0.001）。可见三个实验周期对于走班制下学生的学习成效的影响达到显著水平，且都有着中等促进作用。其组间效应值Q=1.457，p＞0.05，说明实验周期的组间效应并不显著。具体见表3。

2.4.3 学科对走班制学习效果的影响

走班制在不同学科背景下对于学生学习成效的影响结果如表4所示，不同学科的效应作用强度从小到大依次为：偏理科类（g=0.502，p＜0.001）＜偏文科类（g=0.309，p＜0.001）＜体育艺术类（g=0.306，p=0.012＜0.05）。其组间检验结果Q=13.294，p＜0.05，说明走班制的实行在不同的学科之间存在显著差异。其中，偏理科类的效应量大于0.5，处在0.5～0.8之间，说明当走班制在偏理科科目实行时有着中上等促进作用，能最大程度促进学生的学习。而偏文科科目以及体育艺术类科目实行走班时，对学生的学习成效起着中等促进作用且二者差异较小。

2.4.4 能力分层情况对走班制学习效果的影响

进一步分析能力分层内部的不同分层情况对学生的学习成效的影响，由表5可知，不论走班制下能力分层教学内部分为几层，都对学生的学习成效有着中等促进作用，其中教学的效应作用强度从小到大依次为：分三层以上（g=0.261，p＜0.05）＜分三层（g=0.357，p＜0.001）＜分两层（g=0.390，p＜0.001）。其组间效应值Q=6.169，p＜0.05，说明能力分层内部的相关情况对于走班制的影响存在显著差异。

2.4.5 班级规模对走班制学习效果的影响

不同的班级规模对走班制的成效影响结果如表6所示。不同班级规模的效应量均处于0.2～0.5之间，均对走班制下学生的学习成效有着中等促进作用。从具体的效应值来看，班级规模的效应作用强度从小到大依次为：0～30人（g=0.221，p＞0.05）＜61～120人（g=0.230，p＜0.001）＜120人以上（g=0.301，p＜0.001）＜31～60人（g=0.474，p＜0.001）。其组间效应值Q=15.424，p＜0.05，说明不同班级规模之间的效果差异显著，走班制下学生的学习效果受到班级规模的调节作用。